Themes – Ideas – Steps

ELM is organized into Themes (an overarching branch of mathematics), which are then divided divided into different Ideas (mathematical concepts). Each Idea has a certain number of Steps that use carefully sequenced activities to build children’s understanding of the concept. Click on any of the icons below to learn more about at Theme and its associated Ideas and Steps.

Number Concept

Chuck Number Concept

In this theme, students are encouraged to see ‘number’ as a set or a collection of objects. ELM’s activities are intended to develop students’ fluency in recognizing numbers, comparing numbers, adding and subtracting numbers, decomposing numbers into either a sum or difference of two numbers, and understanding the place value of numbers. Students also familiarize themselves with mathematical symbols and vocabulary.

Most of the steps in this theme focus on the numbers 1-9. This gives students the opportunity to learn the concept in a way where they can verify the answer for themselves by using their fingers.

Count

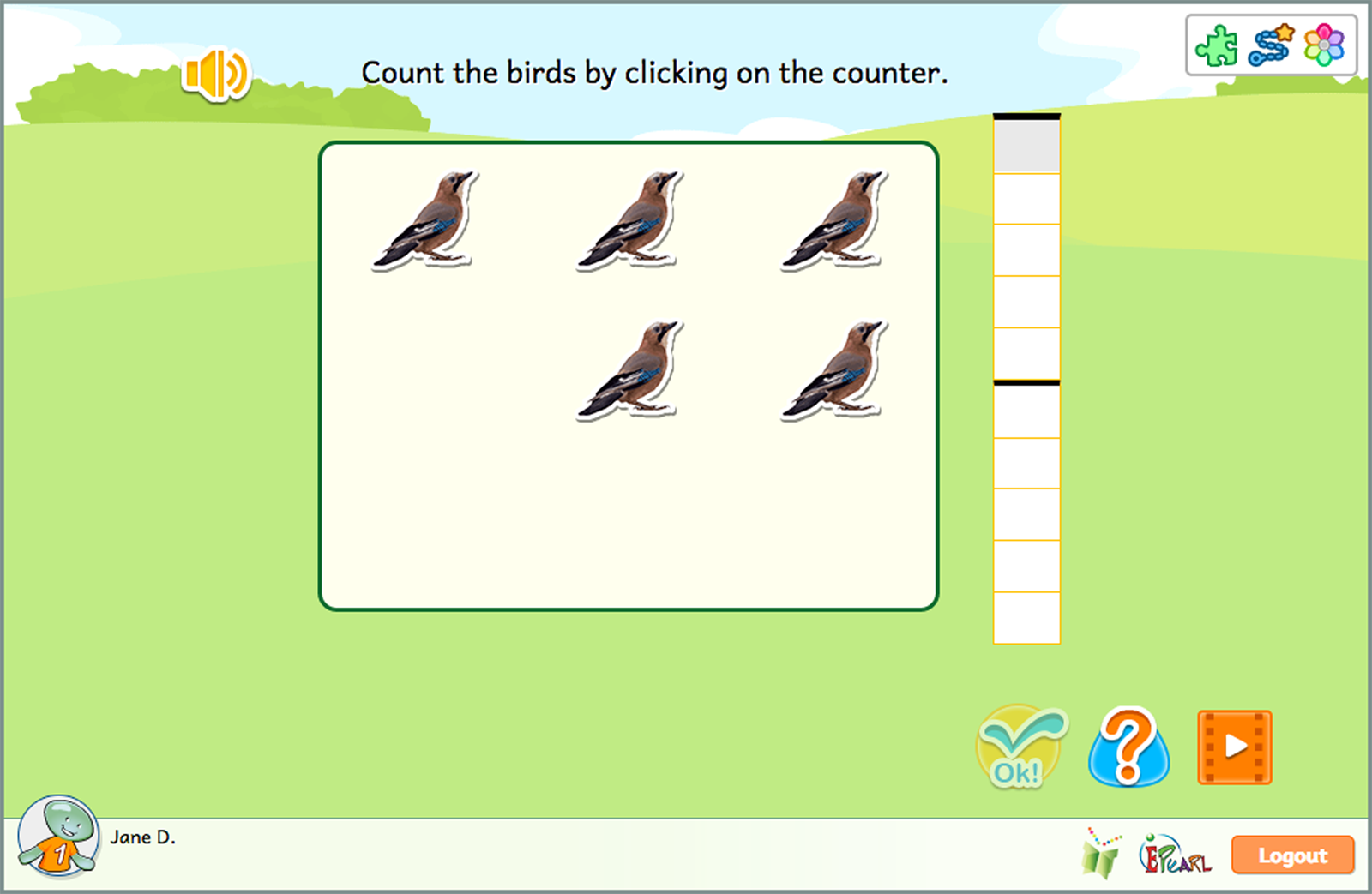
Counting Activity Screenshot

The Count idea helps students become familiar with the basic numerals (1 through 9) and the quantity each represents. The idea’s steps are structured to move from concrete to abstract by means of counting a set of objects. By completing the steps, students also practice subitizing, the ability to instantly recognize the number of objects in a set of objects presented without any conscious counting.

The Count idea has five steps:

  1. Count the birds by clicking on them.
  2. Count the birds by using the counter.
  3. Count the birds using the counter then choose the number from the number bar.
  4. Place the number of birds that Chuck asks for in the field.
  5. Choose the number of birds from the number bar.

Compare

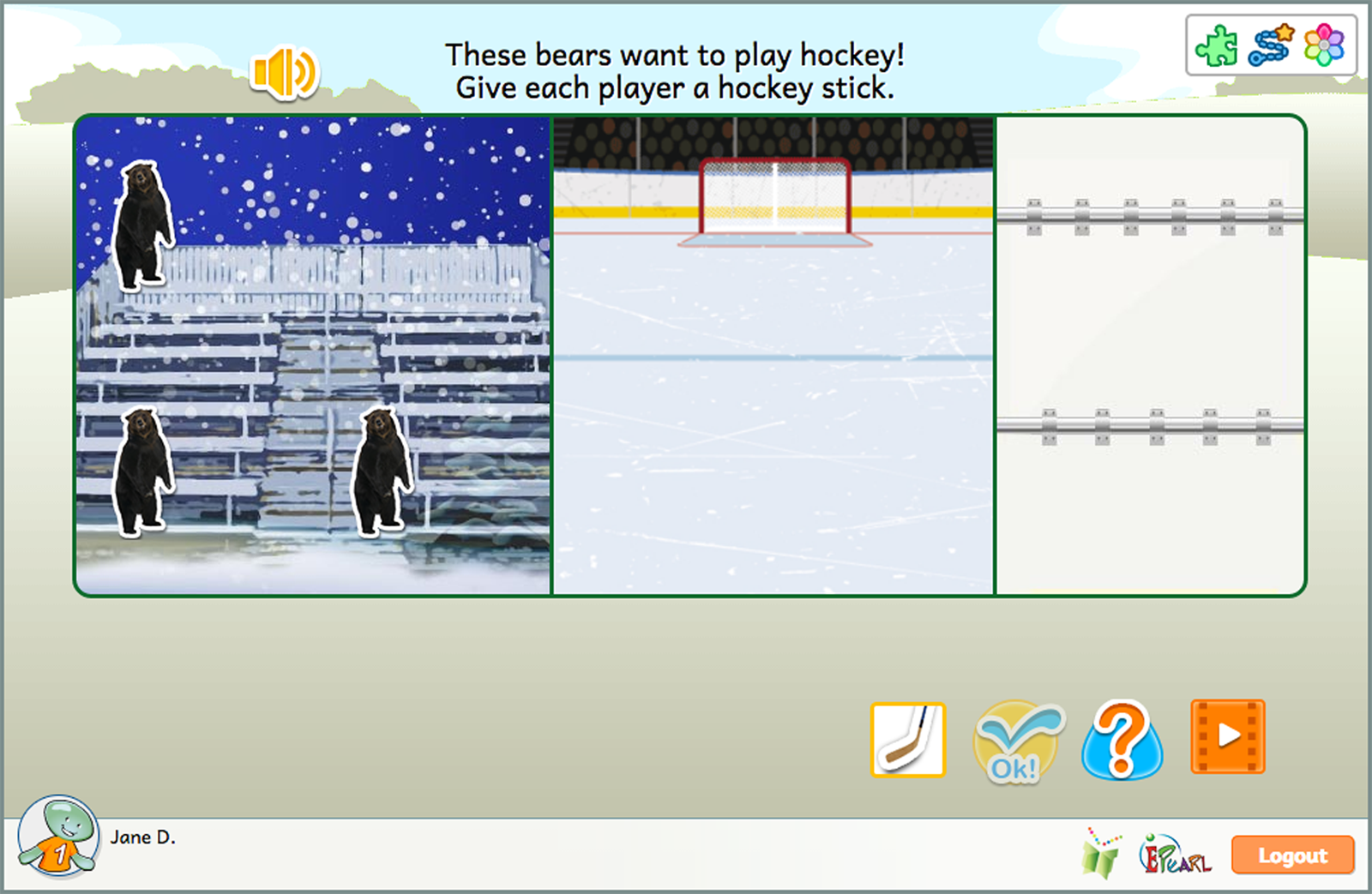
Comparing Activity Screenshot

Students will be asked to count two sets of objects: bears and hockey sticks. They are asked to compare these two sets of objects and determine if they are equal or whether one integer is larger or smaller than the other.

These activities expose students to both natural language and mathematical symbols that express and compare the cardinality of two sets.

The Compare idea has four steps:

  1. Give each bear a hockey stick. Choose the number from the number bar. The system provides ways of stating the expression of equality.
  2. Choose the number of bears and sticks from the number bar. Match bears to sticks. Choose the correct expression using symbols (<, >, =) and words.
  3. Choose the number of bears and sticks from the number bar. Match bears to sticks. Choose the correct expression using symbols (<, >, =) only.
  4. Place number of bears then place number of sticks to match the expression given.

Add

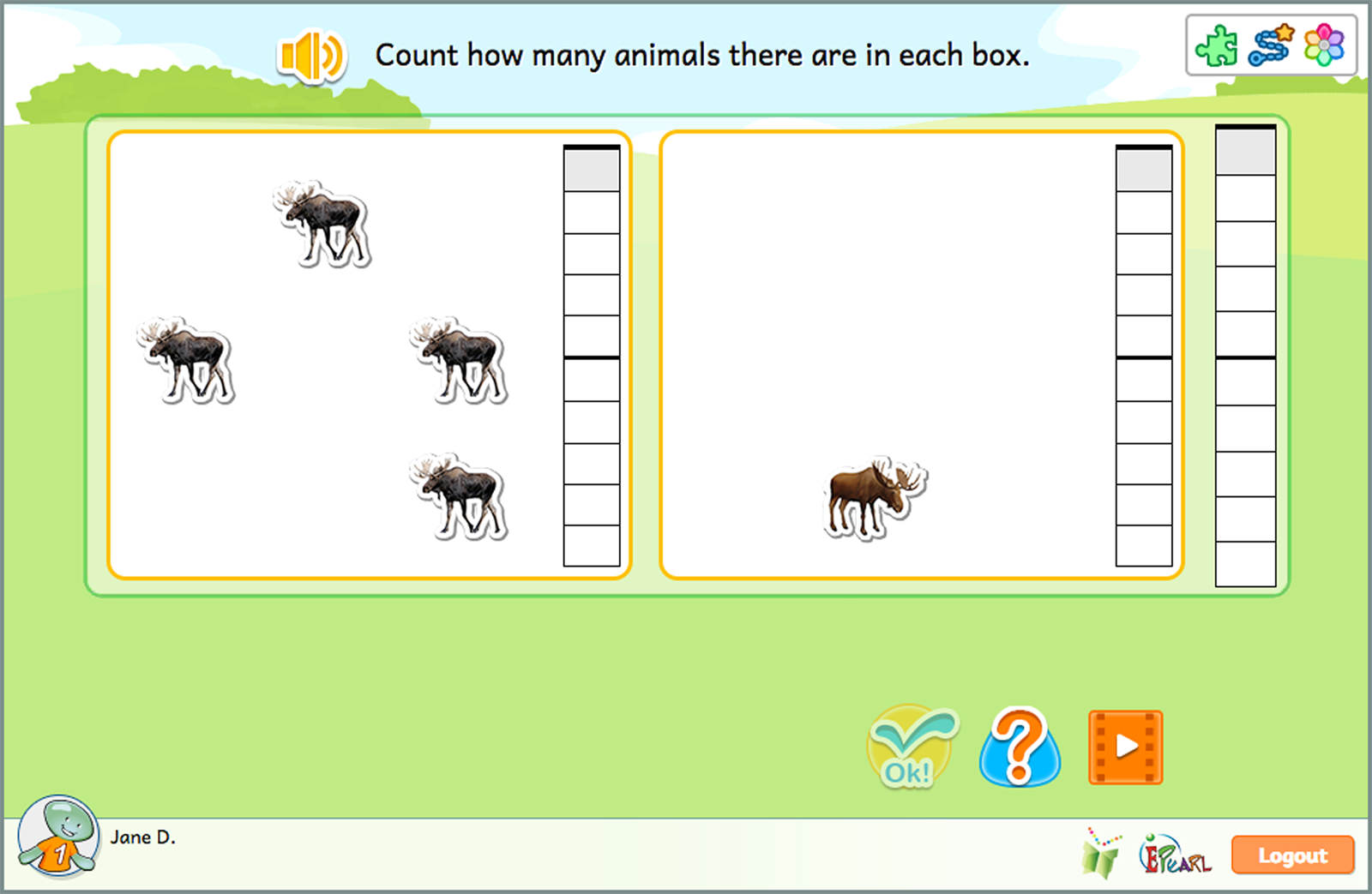
Adding Activity Screenshot

The Add idea requires students to add the cardinality of two sets of animals. They see that the resulting number is the “sum” or “total,” which can be represented by an equation. Students first learn to read equations and then later to write these equations by placing the numbers and symbols in the appropriate order.

The steps in Add reuse the counting strategies learned in the Count steps. This includes clicking on objects to count them and the use of counters to represent cardinality. Each set has its own counter; however, this strategy is extended to use an additional counter to represent the total of both sets.

The Add idea has four steps:

  1. Count the moose by clicking on them then choose the total from the number bar.
  2. Choose the number of deer in each picture. Choose the total. The system will display the equation.
  3. Choose the number of elk in each picture. Choose the total. Build the equation themselves.
  4. Place the deer in each picture to match the given equation.

Subtract

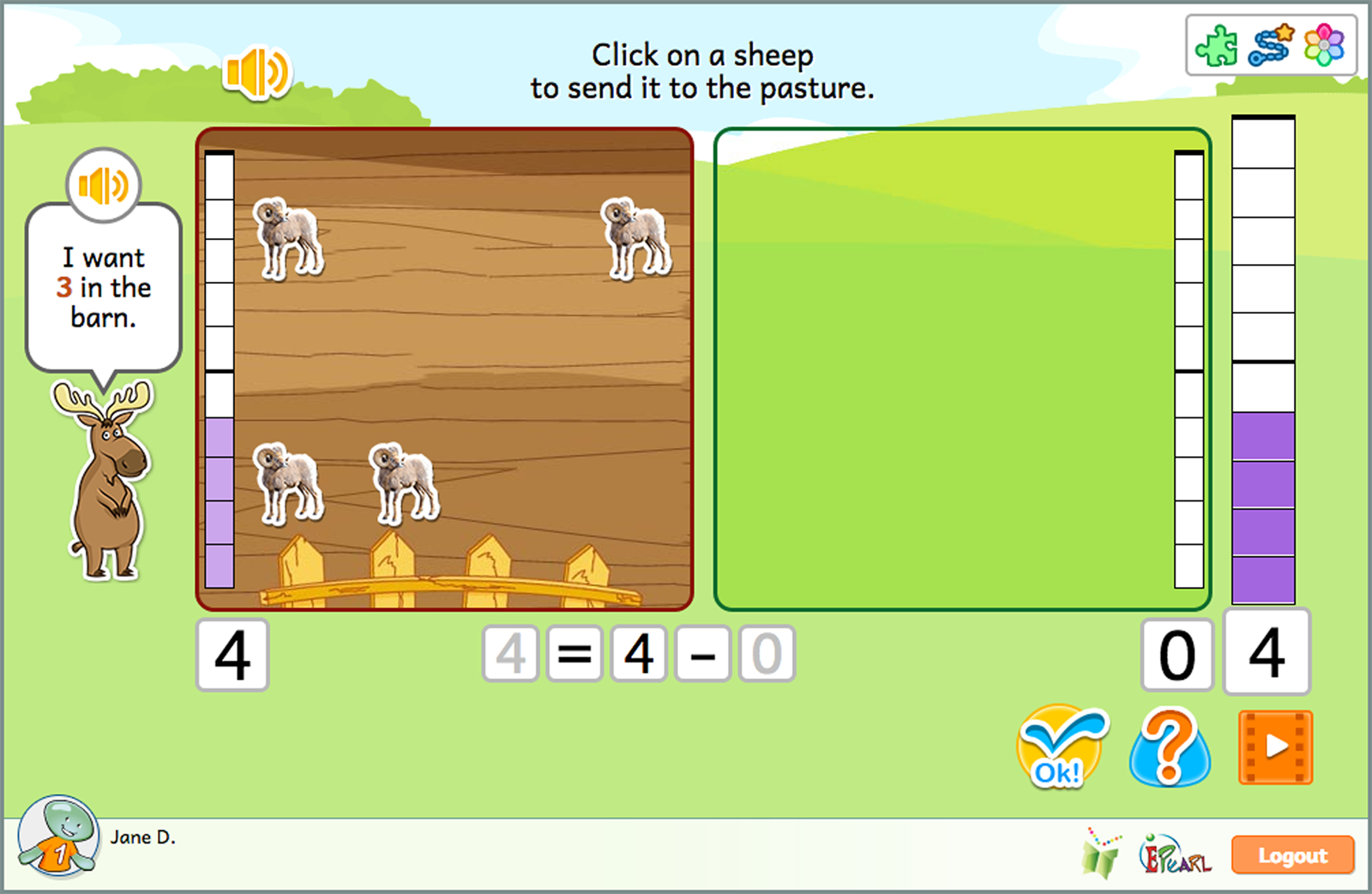
Subtracting Activity Screenshot

The Subtract idea focuses on the process of taking away. In the steps, the student will initially see all animals in one set. They have to count how many are in the set and note the empty second set. This way, the student learns to associate 0 as the count of the empty set.

In the later steps, this process will be associated with an equation. This equation is a symbolic representation of the state of the sets, and the ‘take away’ process that occurred.

The Subtract idea has five steps:

  1. Count the goats in the barn using the number bar. Send the number of goats that Chuck asks for to the pasture by clicking on them.
  2. Count the buffalo in the barn and pasture. Send the correct number of buffalo to the pasture. The system will provide and update the equation.
  3. Count the muskoxen in the barn and pasture. Send the correct number of muskoxen to the pasture. Correct the equation themselves.
  4. Count the Dall sheep in the barn. Add sheep to the pasture to match the total number requested. Correct the equation themselves.
  5. Count the sheep in the barn. Send sheep to the pasture, until the number that remains in the barn matches Chuck's directions. Correct the equation themselves.

Decompose

Decompose Activity Screenshot

The Decompose Idea focuses on integer decomposition or partition. Students are presented with a set of beavers. They must partition this total by separating the beavers into two different sets by deciding which beavers are in the grass or water region.

Later steps include a table where students are tasked with completing the missing line. This demonstrates their understanding of the patterns in the table by selecting a missing value.

The Decompose idea has four steps:

  1. Click on beavers to send the correct number 'swimming'.
  2. Click on beavers to send them swimming until they match the missing line in the decomposition table. Choose the number from the number bar (2 times per puzzle piece).
  3. Choose the number of beavers in the dam based on the missing line in the decomposition table. Then choose the number of beavers swimming.
  4. Choose the number of beavers in the dam and swimming based on the missing line in the decomposition table. The system will display this as an equation.

Place Value

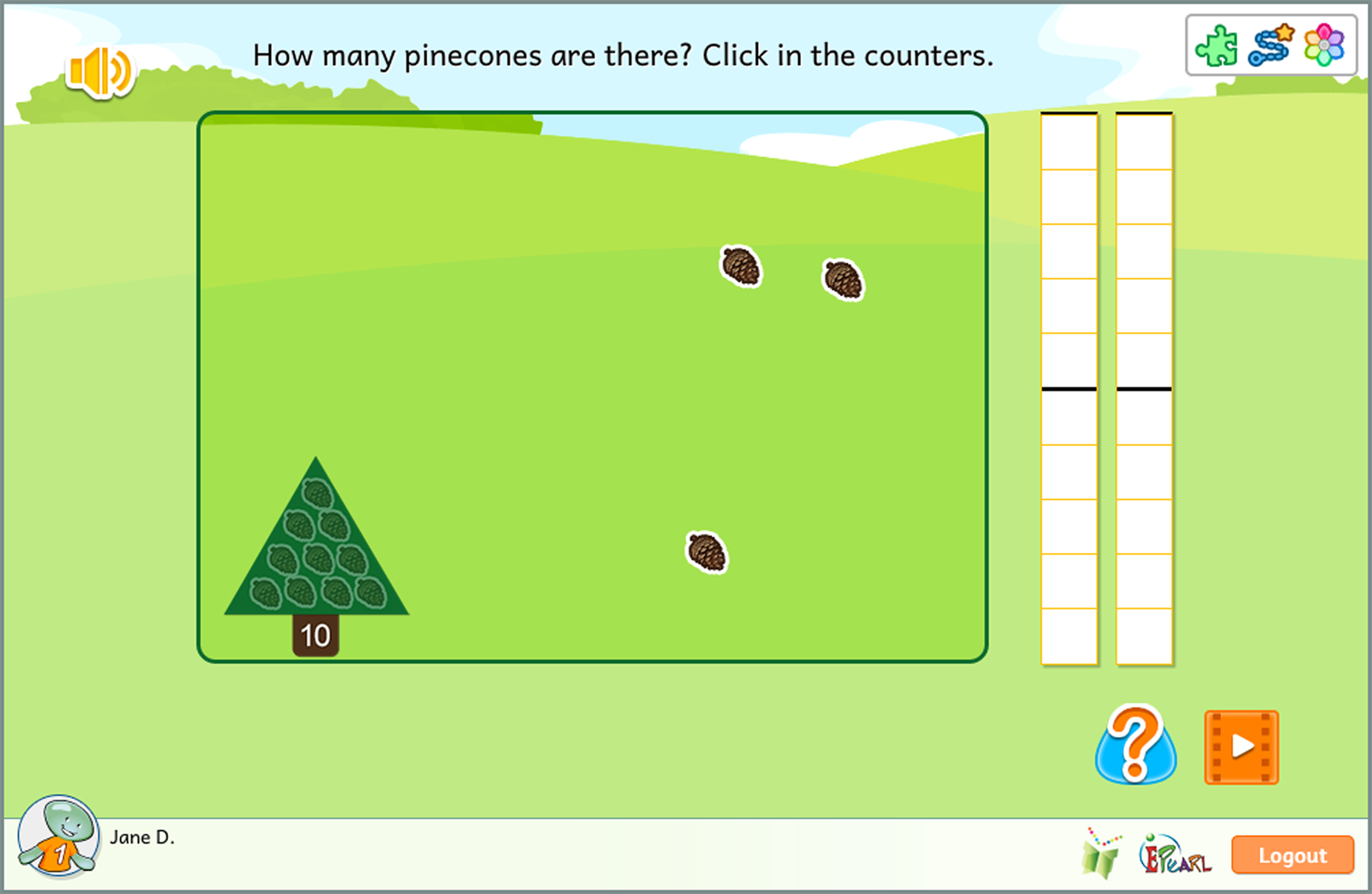
Place Value Activity Screenshot

The Place Value idea helps students realize that numbers beyond 9 but less than 100 have two ‘parts’: there is a number of ‘10s’ combined with a number of ‘1s’. The goal is to have students understand that one ‘ten’ is equal to ten ‘ones’. This combined number is read left (tens) to right (ones).

In order to facilitate students’ grasping the notion of place value, ELM associates tens to trees. When ten units - represented as pinecones - are grouped, they become a tree.

The Place Value idea has nine steps:

  1. Indicate how many pinecones there are using the counter(s).
  2. Add or remove counters to match the pinecones in the field. Indicate how many pinecones there are using the counter(s).
  3. Add or remove full counters to match the number of pinecones. Choose how many pinecones there are using the number bar.
  4. Count the number of trees (tens) and pinecones (ones) there are using the number bar. The system will combine both numerals to create one number.
  5. Count the number of pinecones by placing the numerals in one number box.
  6. Add or remove counters to match the pinecones in the field. Choose how many there are using the counter(s).
  7. Flip the cards of a memory card game until they match two numbers to add to the number Chuck asks for.
  8. Add Chuck's pinecones to the pinecones on the left. Write the equation.
  9. Subtract pinecones from the left side to give Chuck the number he wants. Write the equation.

Geometry

Tia Geometry overview

This theme asks students to categorize and distinguish two-dimensional shapes. ELM’s goal is to develop students’ fluency in recognizing shapes and foster students’ own criteria for correctly identifying shapes. To this end, ELM does not list a shape’s attributes. Instead, the student is provided with varying prototypes and they must define their own criteria for what makes a shape a shape. Teachers can have students justify their definitions of shapes during consultations to ensure adequate and robust understanding has unfolded.

Identify Shapes

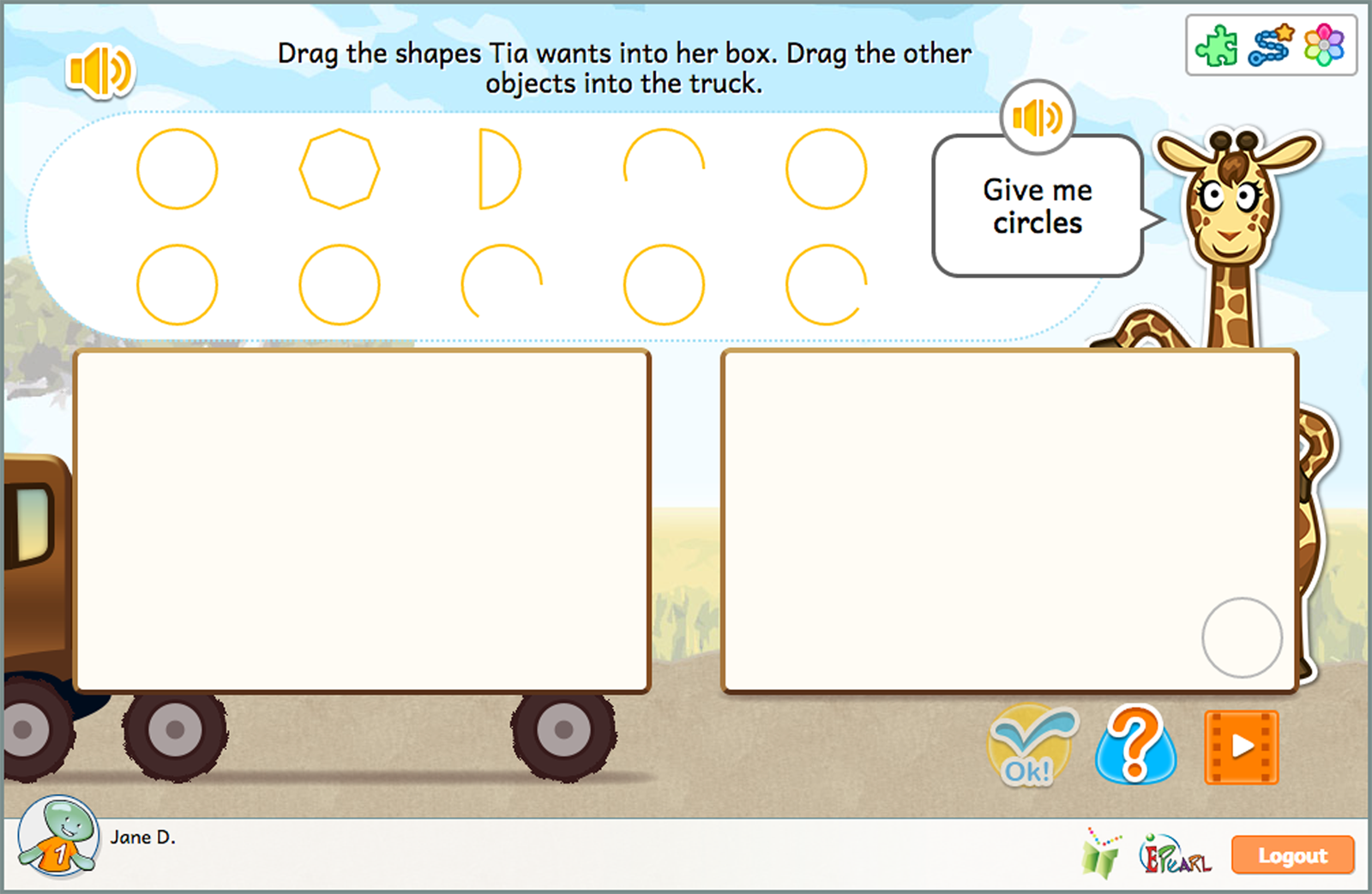
Indintifying Shapes Activity Screenshot

The Identify Shapes idea helps students to realize that there is a set of properties or characteristics that determine if something is a member of a class of shapes.

While ELM does not state any explicit guidelines, students are guided into developing their own understanding that all shapes are closed figures. Furthermore, the boundaries of all shapes considered are composed solely of straight lines, other than for a circle, where the boundary is a curved line. As the steps increase in complexity, students will also note that size is not a property that determines the class of a shape.

The Identify Shapes idea has three steps:

  1. Determine which of the provided assets/img are the two-dimensional shape asked for by dragging it into the appropriate box.
  2. Determine which of the provided assets/img are the two-dimensional shape asked for by dragging it into the appropriate box, with the added challenge of seeing some bigger shapes.
  3. Determine which of the provided assets/img are the two-dimensional shape asked for by dragging it into the appropriate box, with the added challenge of seeing some rotated shapes.

Patterns

Ivan Patterns overview

In early primary grades, students are expected to develop their skills in recognizing the changing attributes in patterns, especially determining the rule for a repeating pattern. Students typically express their understanding by recognizing, continuing, completing and creating patterns. ELM aids the development of their skills in identifying regularity and building sequences.

Translate Patterns

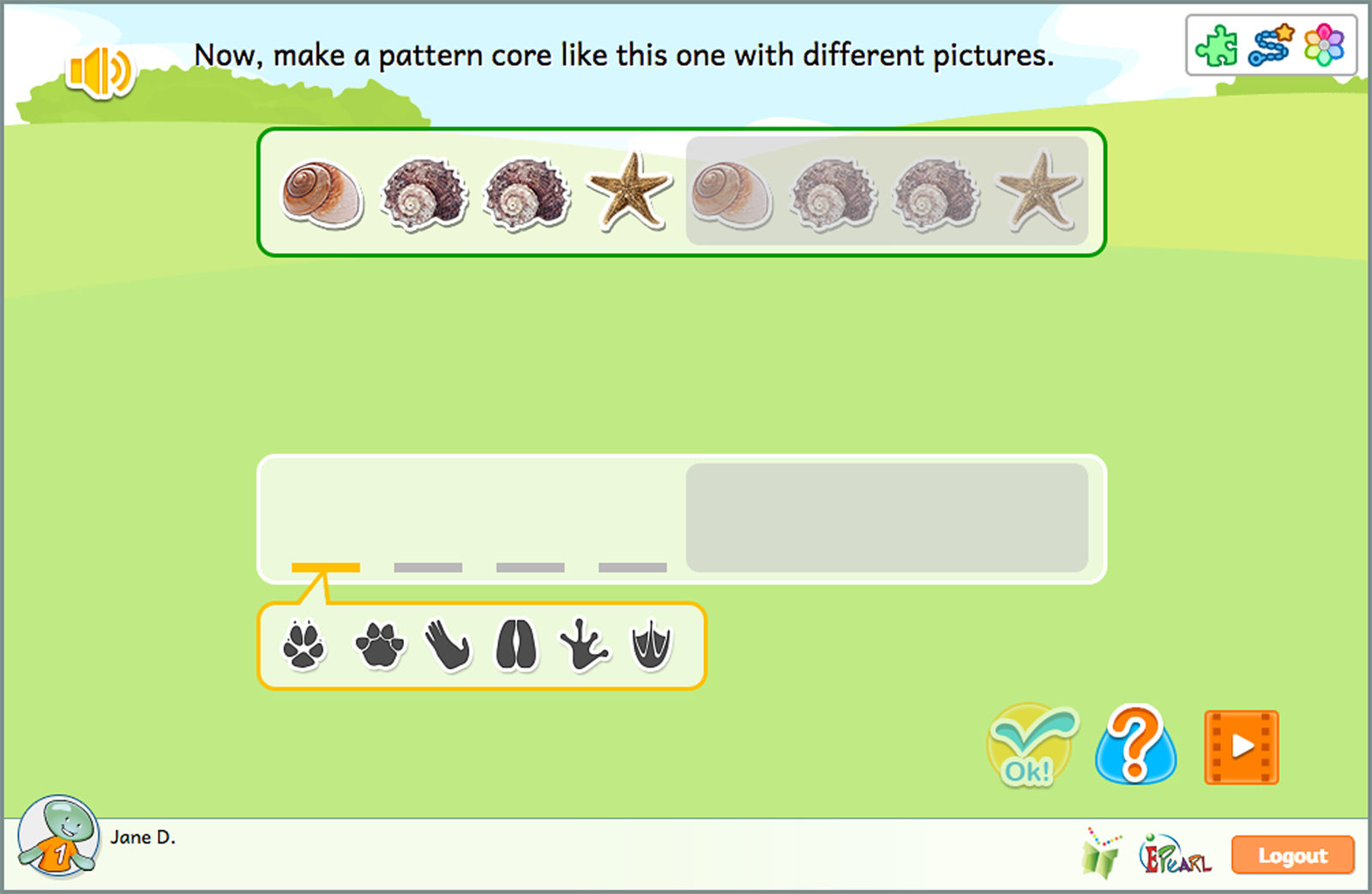
Translating Activity Screenshot

This idea is recommended as a continuation following the development of basic pattern copying, completion and continuation skills.

There are two main objectives for this Idea. The first is developing students’ ability to identify the repeating portion – the core, or unit of repeat. The student is asked to extend this understanding of the core structure in the second objective, which is abstracting the pattern. Students demonstrate this by recreating the pattern using a new set of objects.

The Translate Patterns has one step:

  1. Identify the pattern core. Recreate the pattern using different objects.

Data

Kiros Data overview

In grade 1, students are expected to ask or respond to questions, organize data, and interpret data using graphs and tables, with their teacher’s guidance.

To support students’ development of these skills, this theme presents situations where the answer is not instantly obvious. In order to make sense of the situation, the student is required to organize data according to common attributes and represent a tally using graphs and tables. This task connects the situation to the graphic displays.

Bar Graphs and Tables

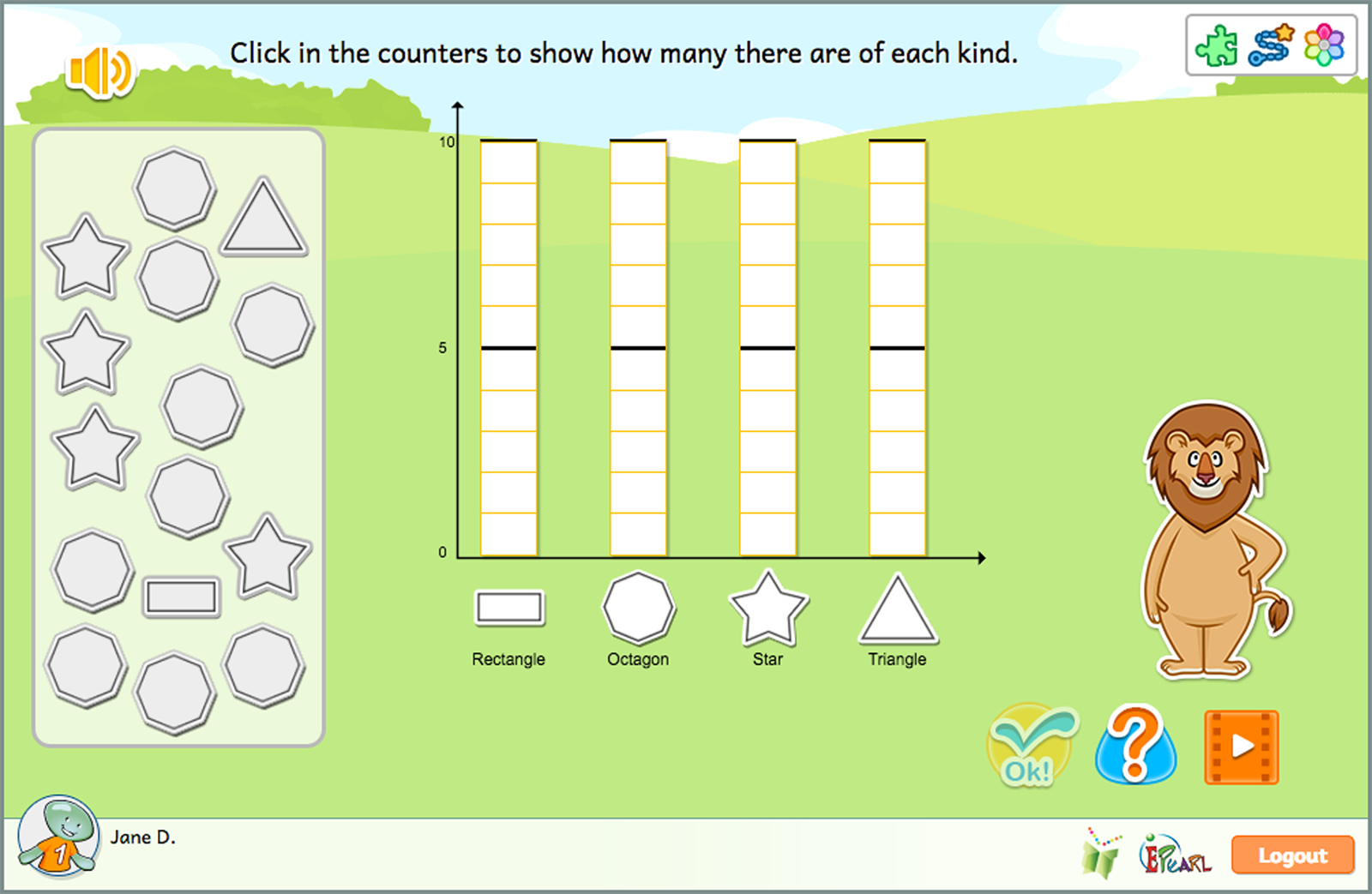
Graphs and Tables Activity Screenshot

The purpose of this Idea is support students’ ability to interpret and display data using bar graphs and tables. The student is provided with a context and they are expected to count and represent that tally using pictures, counters and numerals. Then, the student discovers that a bar graph is useful for organizing data into categories to determine the relative sizes at a glance. As well, students learn that a table can be useful to quickly count the total.

The Bar Graph and Tables idea has two steps:

  1. Identify the number of categories in a pile of objects. Label a bar graph. Fill in a bar graph to match the pile of objects.
  2. Identify the number of categories in a pile of objects. Label a bar graph. Fill in a bar graph to match the pile of objects. Complete a table using the information in a bar graph.

Number Line

Matilda Number Line overview

Number Line provides a different understanding of the concept of numbers explored earlier in the Number Concept theme.

By focusing on the position on a line, students see another concrete method for counting, comparing, and ordering numbers. The number line helps students see that counting up is related to increases in quantity and counting down is related to decreases in quantity.

As well, students see that positive and negative displacements indicate movement in opposite directions along a number line, giving them a new interpretation of addition and subtraction. The use of a standard size of units (step length) also encourages students to discuss the use of different systems of “units”(e.g. mm, cm, m, inch, foot, yard) that lead to different correct numerical answers.

Number as Displacement

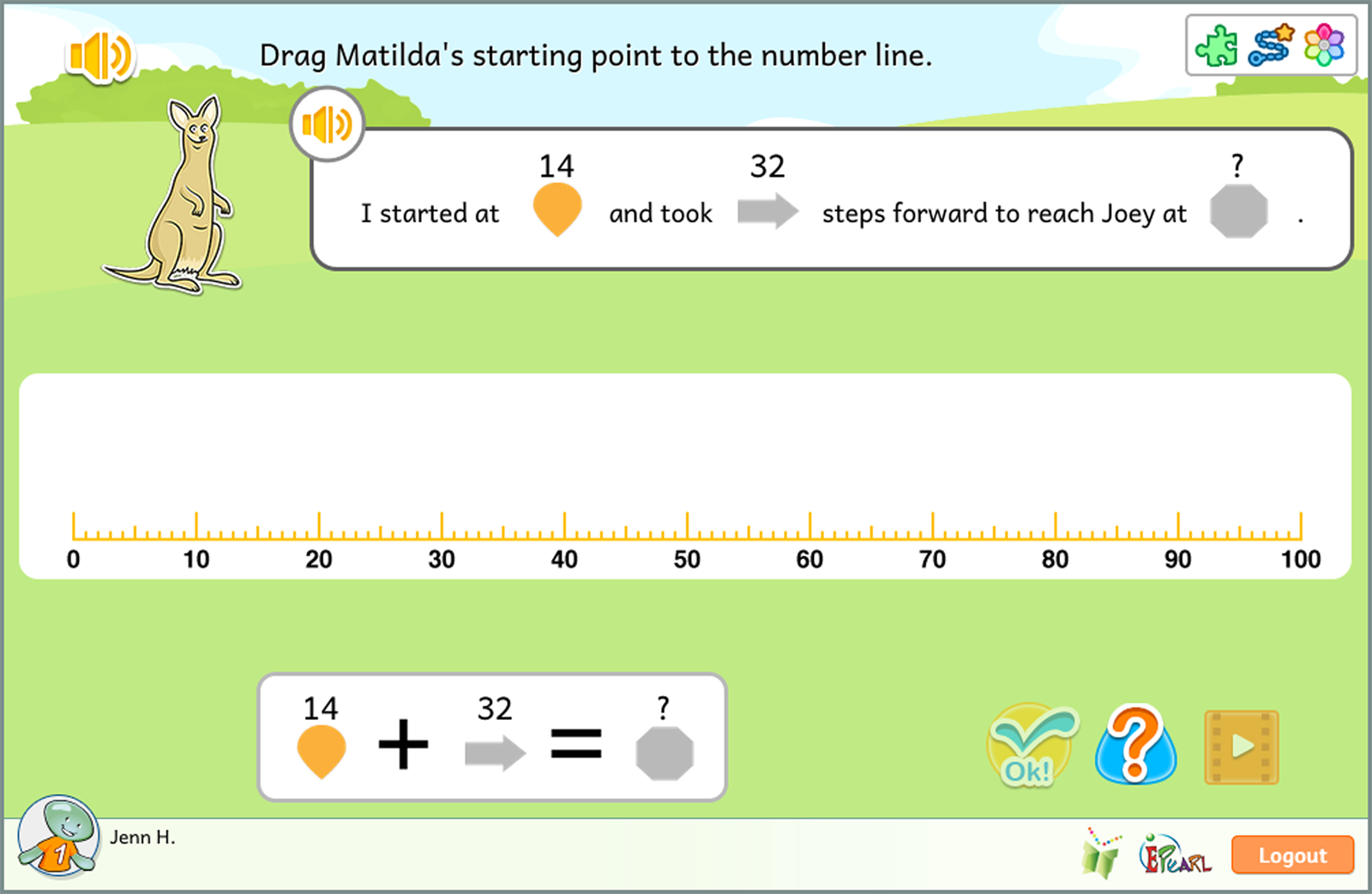
Graphs and Tables Activity Screenshot

This Idea works with three numbers: the starting point (a), the displacement (b), and the ending point (c), which are presented by the equation “a + b = c” or “a – b = c”. Students are given two out of these three numbers. Students first determine what each given number corresponds to physically on the number line. Then, the student can use the physical number line as an aid in determining the missing third value.

The Number as Displacement idea has one step:

  1. Place a marker of the start or end position on a number line. Create the displacement by combining 1, 5 or 10 unit blocks.