Survol d'ORME
Thèmes - Idées - Activités
Le logiciel ORME est divisé en Thèmes (qui correspondent à des branches générales des mathématiques), lesquels se subdivisent eux-mêmes en différentes Idées (qui correspondent à autant de concepts mathématiques). Chaque Idée comporte un certain nombre d'Activités organisées selon une séquence qui permet à l'enfant de construire sa compréhension du concept qui y est enseigné. Cliquez sur n'importe laquelle des icônes ci-dessous afin d'en apprendre davantage sur un Thème et les Idées et Activités qui y sont associées.
Concept de nombre
Dans le thème Concept de nombre, les élèves sont encouragés à voir un " nombre " comme un ensemble ou une collection d'objets. Les activités d'ORME sont conçues afin que les élèves acquièrent une certaine maîtrise lors de la reconnaissance des nombres, de la comparaison de nombres, de l'addition et de la soustraction de nombres, de la décomposition de nombres soit en une somme ou une différence de deux nombres, ainsi que de la compréhension de la valeur de position des chiffres. Les élèves se familiarisent également avec les symboles et le vocabulaire propres aux mathématiques.
La plupart des activités de ce thème se concentrent sur les chiffres de 1 à 9. Les élèves ont ainsi l'occasion d'apprendre le concept avec l'aide d'exercices où ils peuvent vérifier eux-mêmes leur réponse en comptant sur leurs doigts.
Dénombrement
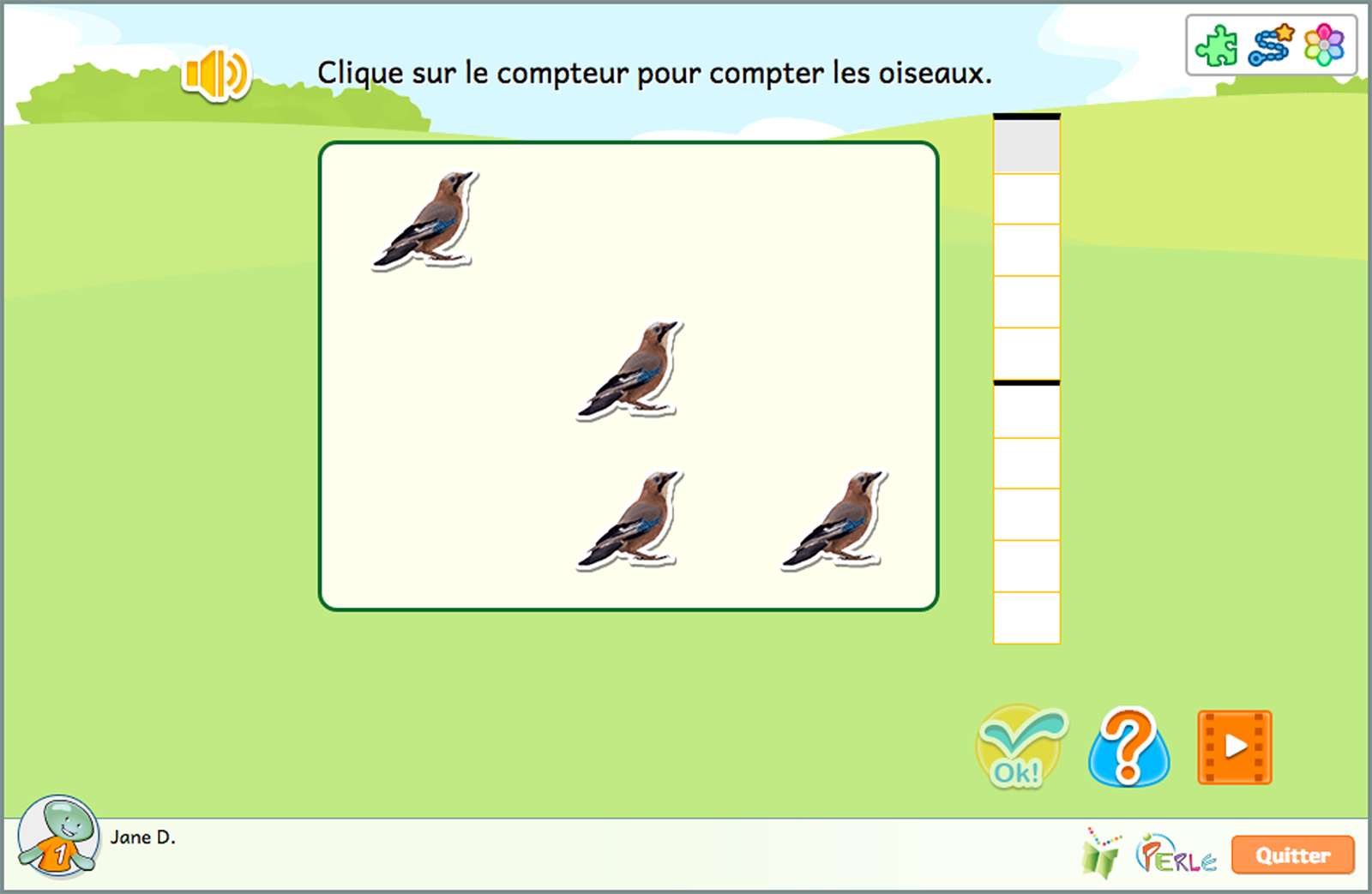
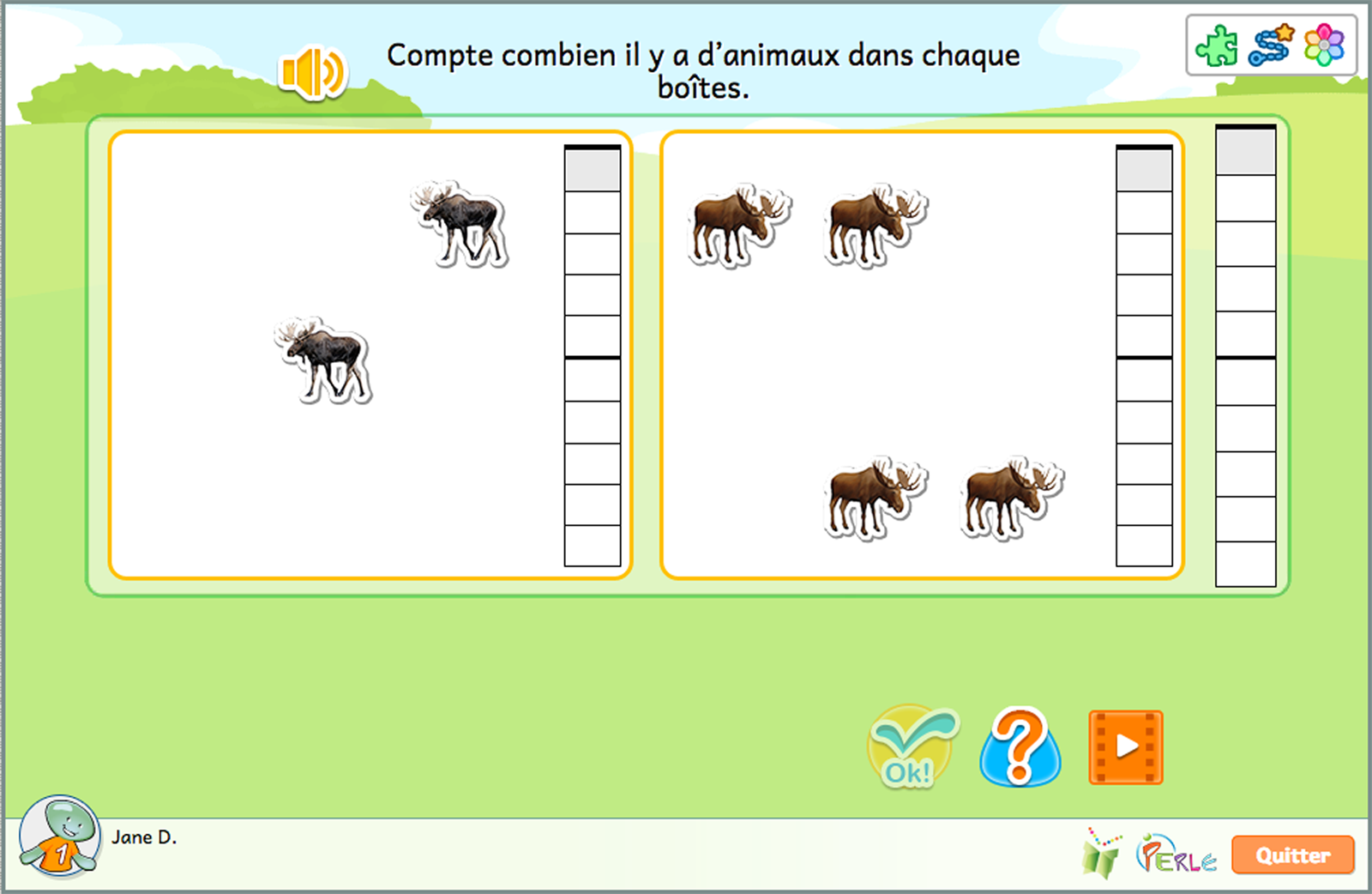
L'idée Dénombrement aide les élèves à se familiariser avec les chiffres de base (de 1 à 9) et la quantité que chacun représente. Les activités y sont structurées de manière à progresser de situations de dénombrement concrètes d'ensembles d'objets vers des situations de plus en plus abstraites. En réalisant ces activités, les élèves pratiquent également la subitisation, c'est-à-dire la capacité de reconnaître instantanément le nombre d'objets qui composent un ensemble d'objets donné sans effectuer de dénombrement conscient.
L'idée Dénombrement comporte cinq activités :
- Dénombrer les oiseaux en cliquant dessus.
- Dénombrer les oiseaux en utilisant le compteur.
- Dénombrer les oiseaux en utilisant le compteur, puis choisir le bon nombre dans la barre de nombres.
- Placer le nombre d'oiseaux demandé par Chuck dans le champ.
- Choisir le nombre d'oiseaux dans la barre de nombres.
Comparaison
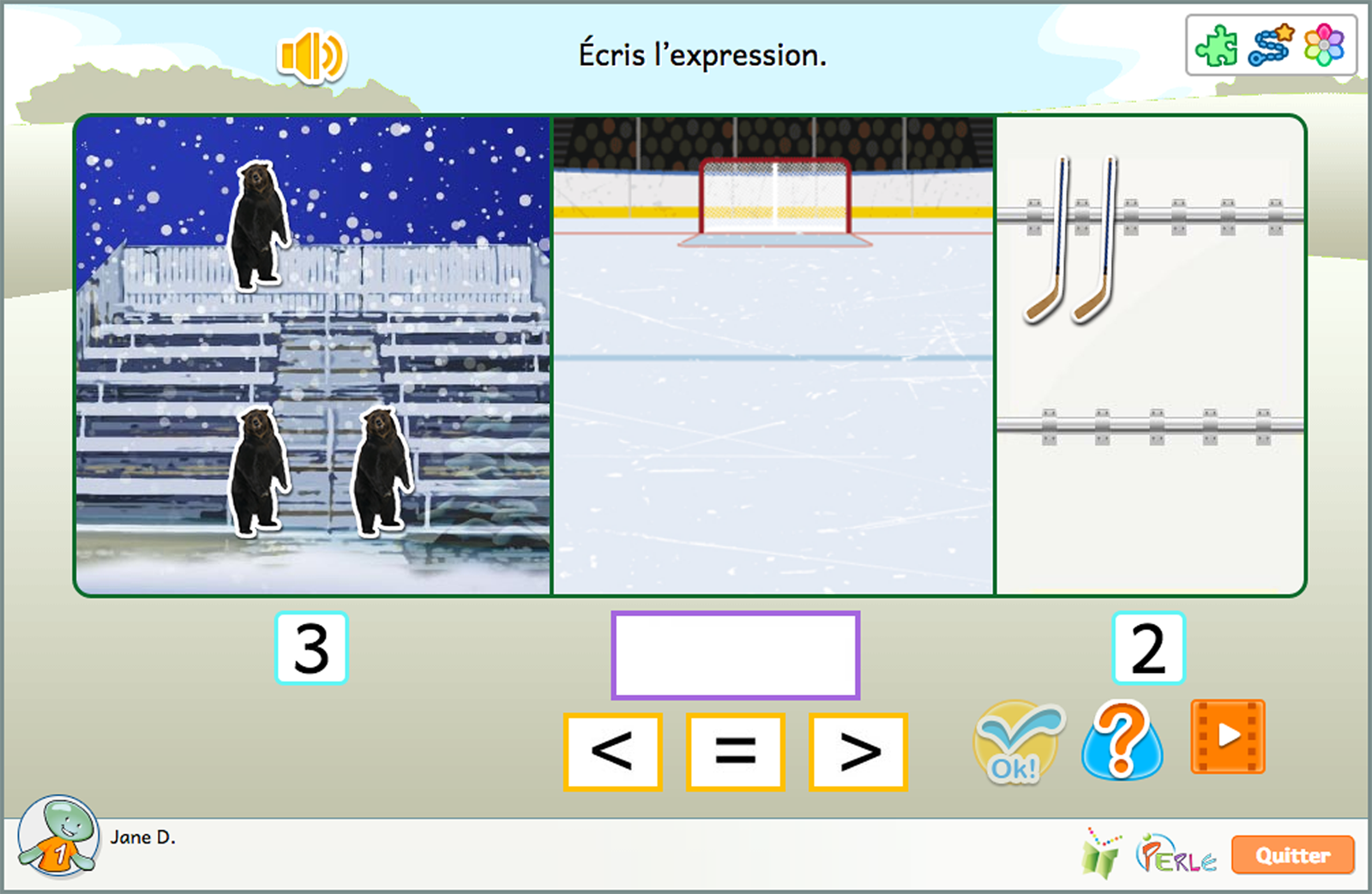
L'élève devra dénombrer deux ensembles d'objets : des ours et des bâtons de hockey. L'élève devra ensuite comparer les deux ensembles d'objets et déterminer s'ils sont égaux ou si l'un des nombres entiers est plus grand ou plus petit que l'autre.
Ces activités mettent l'élève en contact avec le langage naturel et les symboles mathématiques qui permettent de décrire et de comparer la cardinalité de deux ensembles.
L'idée Comparaison comporte quatre activités :
- Donner un bâton de hockey à chaque ours. Choisir le nombre dans la barre de nombres. Le logiciel suggère à l'élève des façons d'exprimer l'égalité.
- Choisir le nombre d'ours et de bâtons dans la barre de nombres. Associer les ours et les bâtons. Choisir l'expression appropriée en utilisant les symboles (<, >, =) et des mots.
- Choisir le nombre d'ours et de bâtons dans la barre de nombres. Associer les ours et les bâtons. Choisir l'expression appropriée en utilisant les symboles (<, >, =) seulement.
- Placer le nombre d'ours et le nombre de bâtons correspondant à l'expression donnée.
Addition
Les activités de l'idée Addition demandent à l'élève d'additionner la cardinalité de deux ensembles d'animaux. L'élève voit que la réponse est un nombre qui correspond à la " somme " ou au " total " et qu'elle peut être représentée au moyen d'une équation. L'élève apprend d'abord à lire les équations, puis il ou elle apprend à écrire ces équations en plaçant les nombres et les symboles dans l'ordre approprié.
Les activités de l'idée Addition reprennent les stratégies apprises dans les activités de l'idée Dénombrement. Ces stratégies comprennent entre autres le fait de cliquer sur les objets pour les dénombrer et l'utilisation de compteurs pour représenter la cardinalité. Chaque ensemble possède son propre compteur; toutefois, un compteur additionnel s'ajoute afin de représenter le total des deux ensembles.
L'idée Addition comporte quatre activités :
- Dénombrer les orignaux en cliquant dessus, puis choisir le total dans la barre de nombres.
- Choisir le nombre de cerfs dans chaque image. Choisir le total. Le logiciel affiche l'équation.
- Choisir le nombre d'élans dans chaque image. Choisir le total. Composer les équations.
- Placer des cerfs dans chacune des images afin qu'elles correspondent à l'équation donnée.
Soustraction
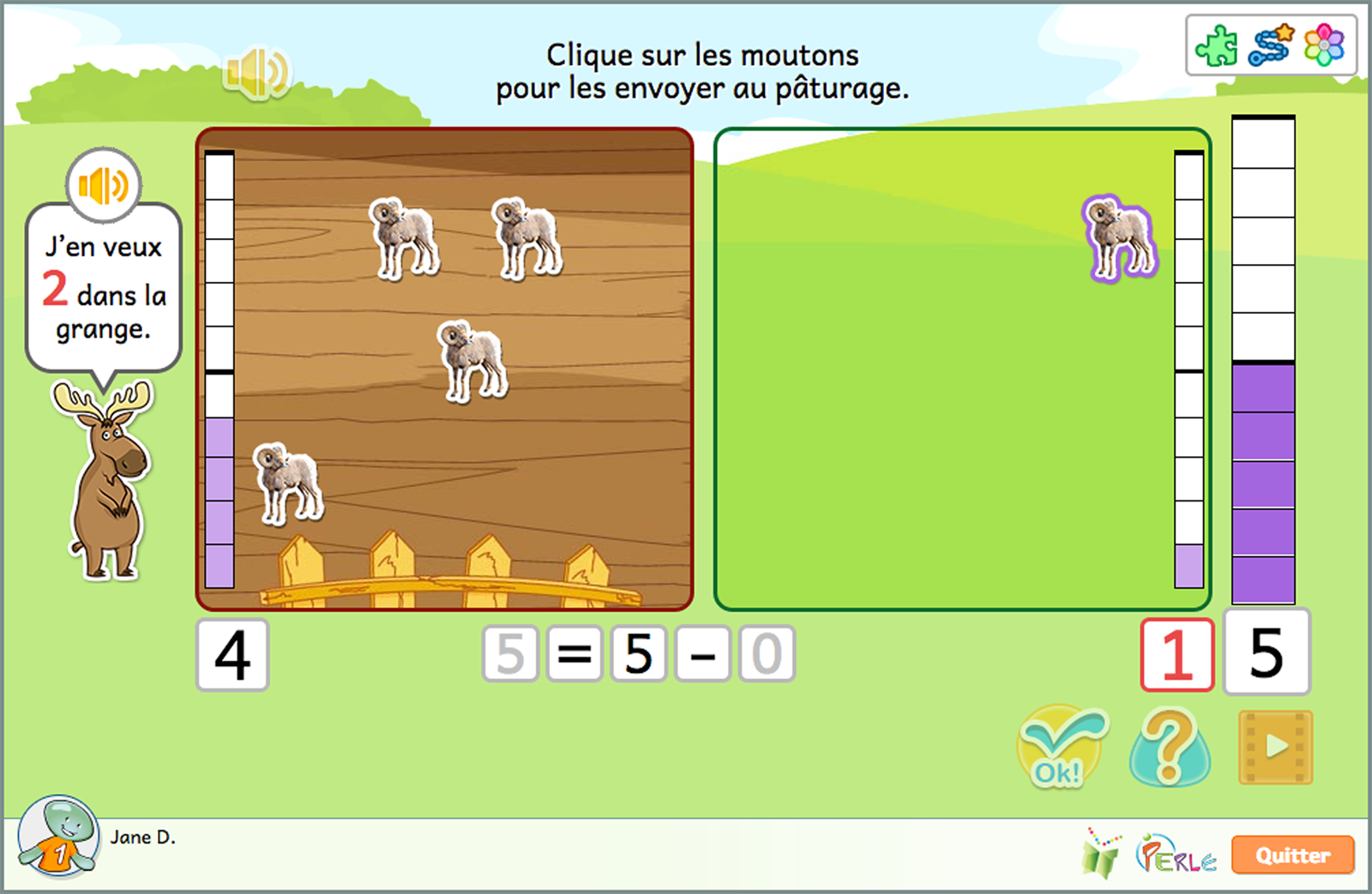
TL'idée Soustraction se concentre sur le processus qui consiste à enlever ou à retirer des éléments. Dans les activités, l'élève verra au départ tous les animaux s'afficher dans un seul et même ensemble. L'élève devra dénombrer les animaux de chaque ensemble et aussi remarquer que le deuxième ensemble est vide. Ceci permet à l'élève d'appendre à associer le symbole 0 au compte d'un ensemble vide.
Lors des activités suivantes, l'opération sera associée à une équation. Cette équation sera la représentation symbolique de l'état des ensembles et de l'opération au cours de laquelle des objets ont été retirés d'un ensemble.
L'idée Soustraction comporte cinq activités :
- Compter les chèvres dans la grange en utilisant la barre de nombres. Envoyer le nombre de chèvres indiqué par Chuck au pâturage en cliquant dessus.
- Compter les bisons dans la grange et au pâturage. Envoyer le bon nombre de bisons au pâturage. Le logiciel fournit l'équation et la met à jour.
- Dénombrer les bœufs musqués dans la grange et au pâturage. Envoyer le bon nombre de bœufs musqués au pâturage. Corriger les équations.
- Compter les mouflons de Dall dans la grange. Ajouter des mouflons au pâturage pour correspondre au nombre total demandé. Corriger les équations.
- Dénombrer les moutons dans la grange. Envoyer des moutons au pâturage jusqu'à ce que le nombre qui reste dans la grange corresponde aux instructions de Chuck. Corriger les équations.
Décomposition

L'idée Décomposition met l'accent sur la décomposition ou la partition de nombres entiers. Le logiciel présente à l'élève un ensemble de castors. L'élève doit diviser le nombre total de castors en deux ensembles différents en décidant quels castors iront dans l'herbe ou dans l'eau.
Les dernières activités comportent un tableau où l'élève a pour tâche de compléter une ligne manquante. L'élève peut ainsi démontrer qu'il ou elle a bien compris les régularités du tableau en sélectionnant la valeur manquante.
TL'idée Décomposition comporte quatre activités :
- Cliquer sur les castors pour en envoyer le bon nombre nager.
- Cliquer sur les castors pour les envoyer nager jusqu'à ce que le nombre corresponde à la ligne manquante de la table de décomposition. Choisir le nombre dans la barre de nombre (2 fois pour chaque pièce de casse-tête).
- Choisir le nombre de castors sur le barrage d'après la ligne manquante de la table de décomposition. Choisir ensuite le nombre de castors qui nagent.
- Choisir le nombre de castors qui sont sur le barrage et qui nagent d'après la ligne manquante de la table de décomposition. Le logiciel affiche l'équation correspondante.
Valeur de position
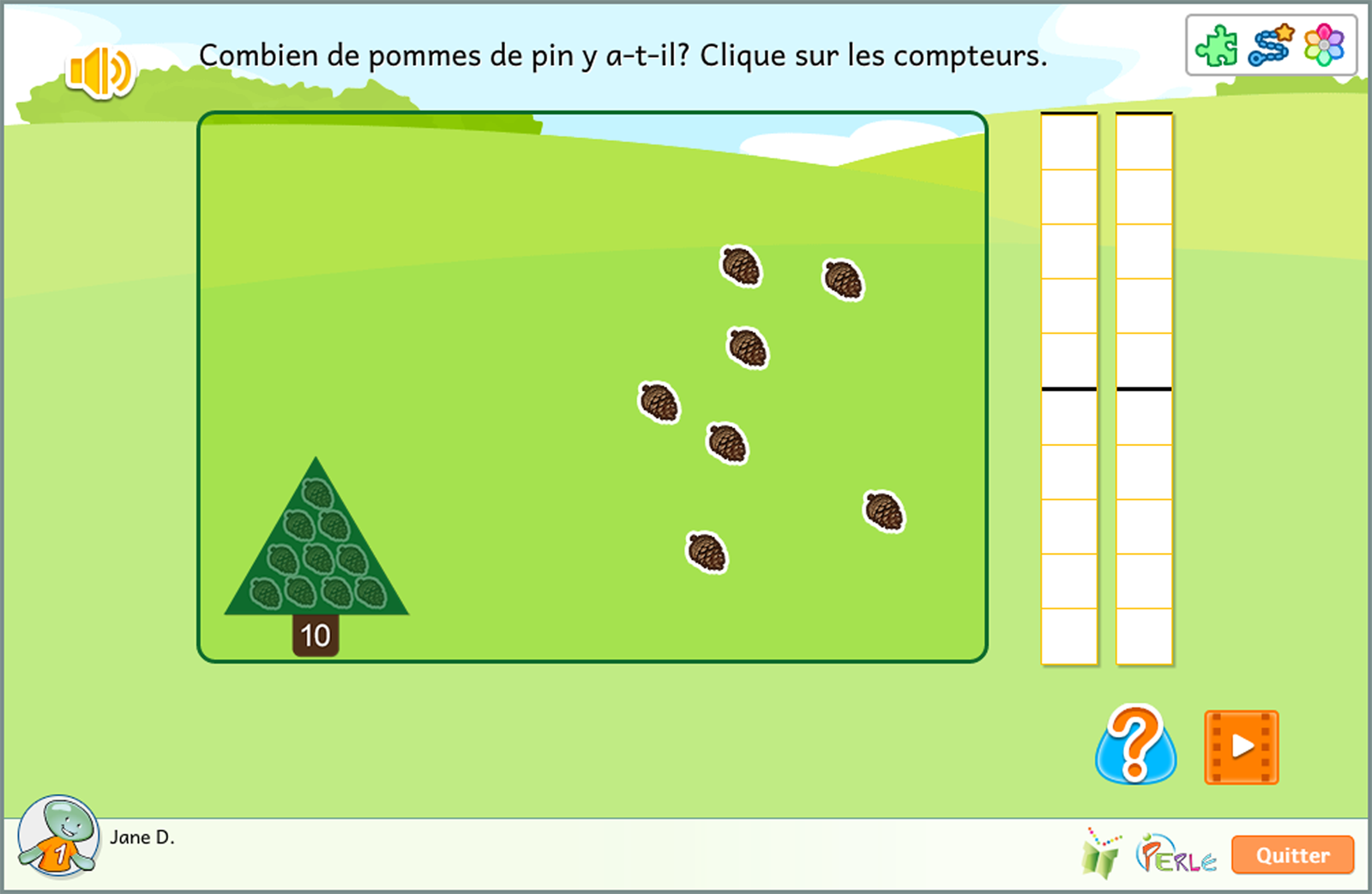
L'idée Valeur de position aide l'élève à prendre conscience que les nombres supérieurs à 9 mais inférieurs à 100 sont composés de deux " parties " : un chiffre à la position des dizaines et un chiffre à la position des unités. Les activités de cette idée visent à faire comprendre à l'élève qu'une dizaine équivaut à dix unités. Le nombre ainsi composé se lit de gauche (dizaines) à droite (unités).
Afin de faciliter la compréhension de la notion de valeur de position, ORME associe les dizaines à des arbres. Lorsque dix unités - représentées par des cocottes - sont regroupées, elles deviennent un arbre.
L'idée Valeur de position comporte neuf activités :
- Indiquer combien de cocottes il y a en utilisant le(s) compteur(s).
- Ajouter ou enlever des compteurs afin qu'ils correspondent aux cocottes dans le champ. Indiquer combien de cocottes il y a en utilisant le(s) compteur(s).
- Ajouter ou enlever des compteurs complets afin qu'ils correspondent au nombre de cocottes. Choisir combien il y a de cocottes en utilisant la barre de nombres.
- Dénombrer les arbres (dizaines) et les cocottes (unités) en utilisant la barre de nombres. Le logiciel combinera les deux chiffres afin de créer un nombre.
- Dénombrer les cocottes en plaçant les chiffres dans une case.
- Ajouter ou enlever des compteurs afin qu'ils correspondent aux cocottes dans le champ. Choisir combien il y en a en utilisant le(s) compteur(s).
- Retourner des cartes du jeu de mémoire jusqu'à ce qu'elles correspondent à deux nombres qui, lorsqu'additionnés, correspondent au nombre demandé par Chuck.
- Ajouter les cocottes de Chuck aux cocottes qui se trouvent à la gauche de l'écran. Composer l'équation.
- Soustraire des cocottes du côté gauche de l'écran pour donner à Chuck la quantité qu'il veut. Composer l'équation.
Géométrie
Dans le thème Géométrie, l'élève doit reconnaître et classer des figures à deux dimensions. ORME a pour objectif de faire en sorte que l'élève maîtrise la reconnaissance des formes géométriques; pour ce faire, le logiciel encourage l'élève à développer ses propres critères pour identifier correctement les figures. C'est la raison pour laquelle ORME ne fournit pas de liste des caractéristiques associées à une figure. Le logiciel propose plutôt à l'élève différents prototypes à partir desquels il ou elle doit définir ses propres critères qui lui permettront de déterminer que telle figure appartient à telle famille de figures. L'enseignante ou l'enseignant peut consulter les élèves et leur demander de justifier leurs définitions des différentes figures afin de s'assurer qu'ils ont acquis une compréhension adéquate et solide des concepts.
Figures planes
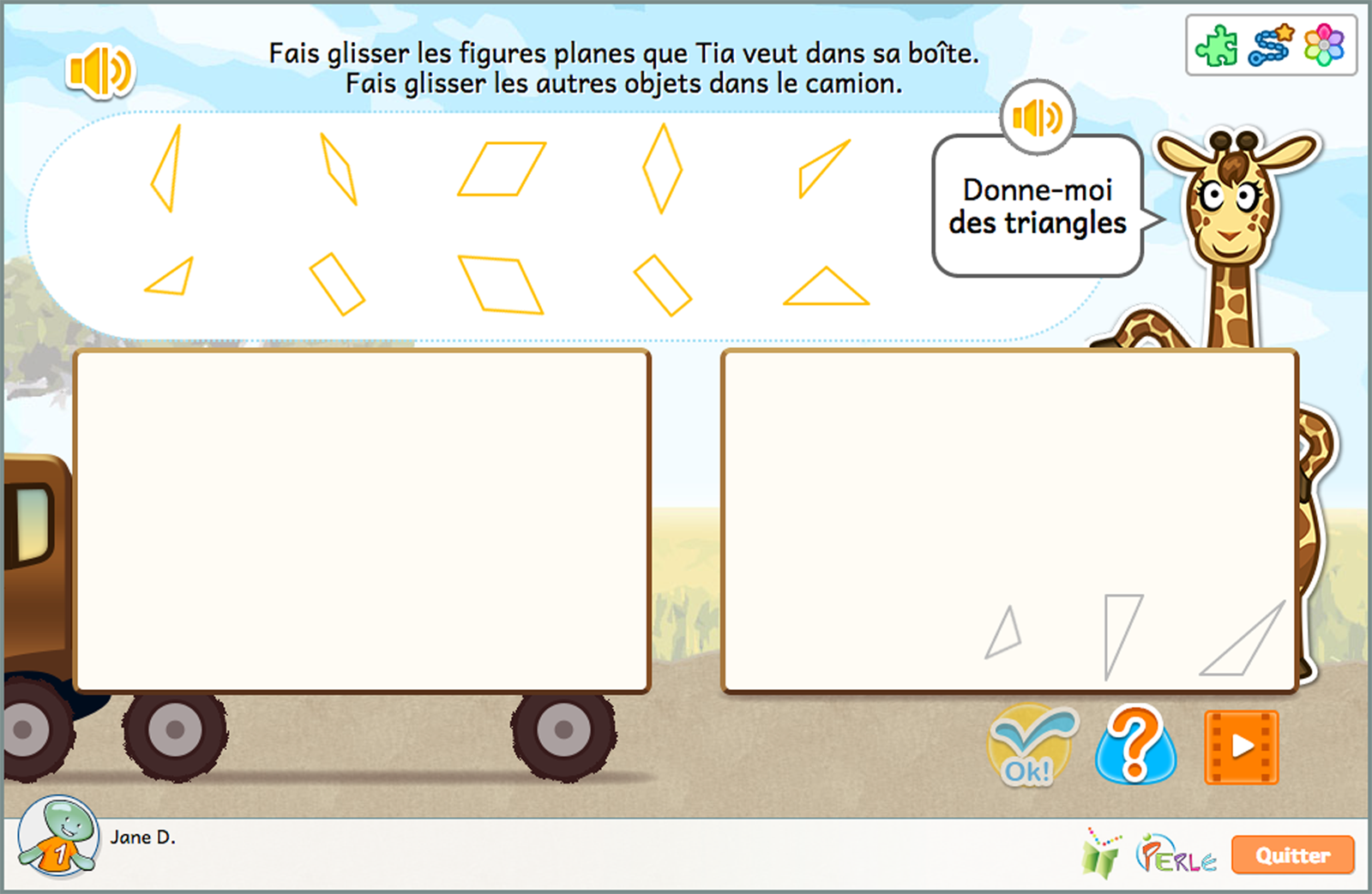
L'idée Figures planes a pour objectif d'aider l'élève à prendre conscience qu'il existe un ensemble de propriétés ou de caractéristiques qui permettent de déterminer si une figure donnée appartient à une famille de figures planes.
Bien qu'ORME ne donne pas de lignes directrices claires, le logiciel guide l'élève afin qu'il ou elle comprenne qu'une figure plane est nécessairement fermée. De plus, les frontières de toutes les figures planes étudiées se composent uniquement de lignes droites, à l'exception du cercle, où la frontière est une ligne courbe. À mesure que les activités deviennent de plus en plus complexes, l'élève remarquera également que la grosseur n'est pas une propriété qui permet déterminer la famille d'une figure plane.
L'idée Figures planes comporte trois activités :
- Déterminer lesquelles, parmi les images proposées, sont des figures planes qui correspondent à la forme demandée en les faisant glisser dans la boîte appropriée.
- Déterminer lesquelles, parmi les images proposées, sont des figures planes qui correspondent à la forme demandée en les faisant glisser dans la boîte appropriée, avec le défi additionnel que certaines formes sont plus grosses que d'autres.
- Déterminer lesquelles, parmi les images proposées, sont des figures planes qui correspondent à la forme demandée en les faisant glisser dans la boîte appropriée, avec le défi additionnel que certaines formes ont subi une rotation.
Régularités

Pendant les premières années du primaire, l'on s'attend à ce que l'élève développe ses compétences afin d'être en mesure de reconnaître les différentes caractéristiques qui peuvent former des régularités, et plus particulièrement de trouver la règle qui permet de répéter cette régularité. L'élève démontre généralement sa compréhension du concept en reconnaissant, en prolongeant, en complétant ou en créant des régularités. ORME aide au développement de ces compétences en demandant à l'élève de reconnaître des régularités et de construire des suites logiques.
Régularités non numériques
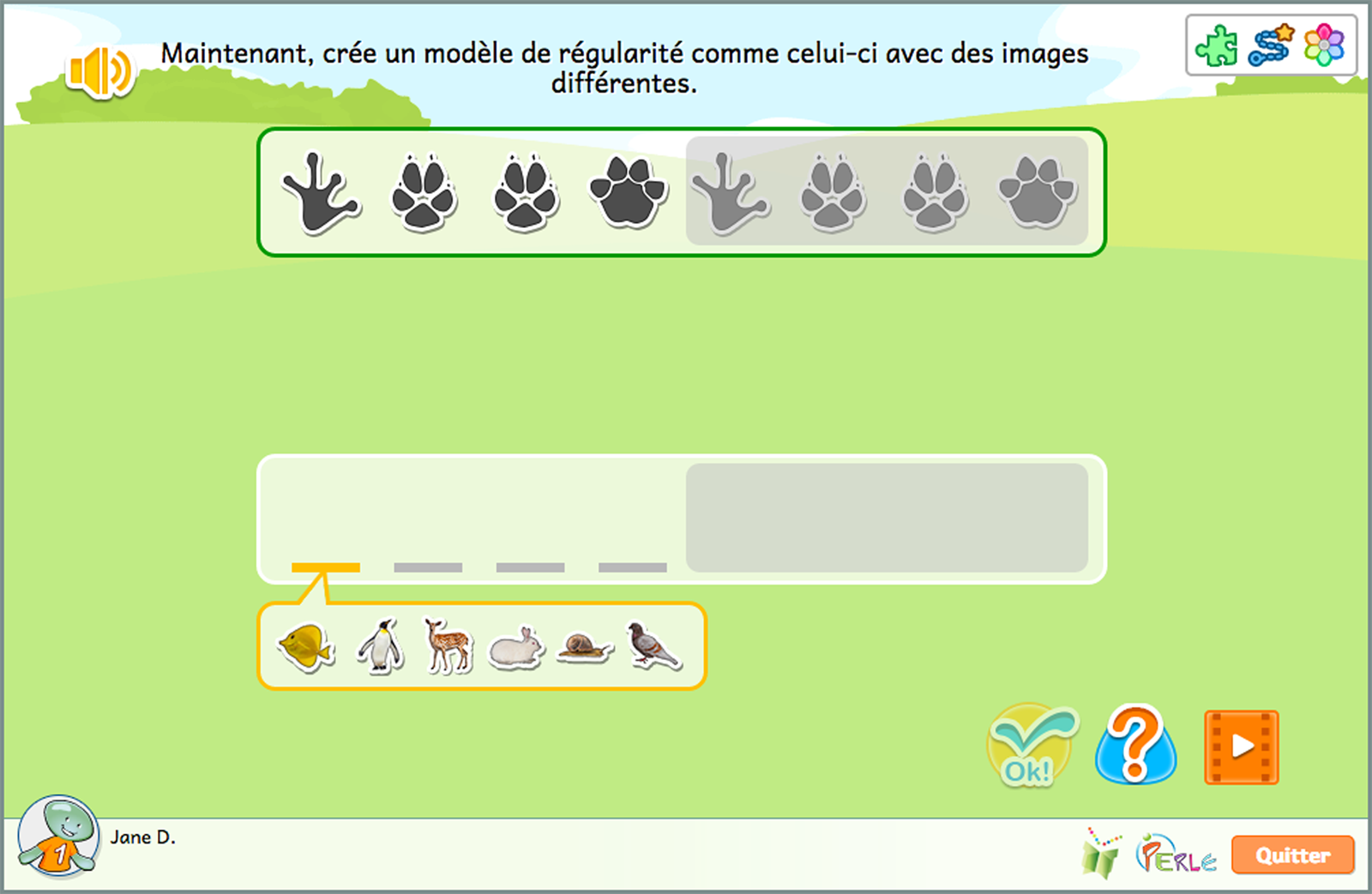
Nous recommandons aux élèves de compléter les activités de l'idée Régularités non numériques afin d'aller plus loin dans le développement des compétences de base requises pour reproduire, compléter et allonger des suites ou des régularités.
Cette idée comporte deux objectifs principaux. Le premier consiste à développer les compétences de l'élève afin qu'il ou elle arrive à identifier la portion qui se répète, c'est-à-dire ce qui est à l'origine de la régularité ou l'unité de répétition de base. Le logiciel amène ensuite l'élève à étendre sa compréhension de la structure fondamentale des régularités avec le deuxième objectif, qui consiste à extraire le motif de la régularité. L'élève démontre qu'il ou elle a compris en recréant la régularité au moyen d'un nouvel ensemble d'objets.
L'idée Régularités non numériques comporte une activité :
- Identifier l'unité de répétition de la régularité. Recréer la régularité en utilisant des objets différents.
Données
En première année, l'on s'attend à ce que l'élève soit en mesure de poser des questions ou d'y répondre, d'organiser des données et d'interpréter des données, le tout au moyen de diagrammes et de tableaux sous la supervision de son enseignante ou de son enseignant.
Afin de stimuler le développement de ces compétences, ce thème présente à l'élève des situations où la réponse n'est pas évidente sur-le-champ. Afin de comprendre la situation, l'élève doit organiser les données en fonction d'attributs communs et présenter visuellement les totaux au moyen de diagrammes ou de tableaux. Cette tâche fait le lien entre l'énoncé de la situation et l'affichage sous la forme de graphiques.
Diagrammes à barres et tableaux
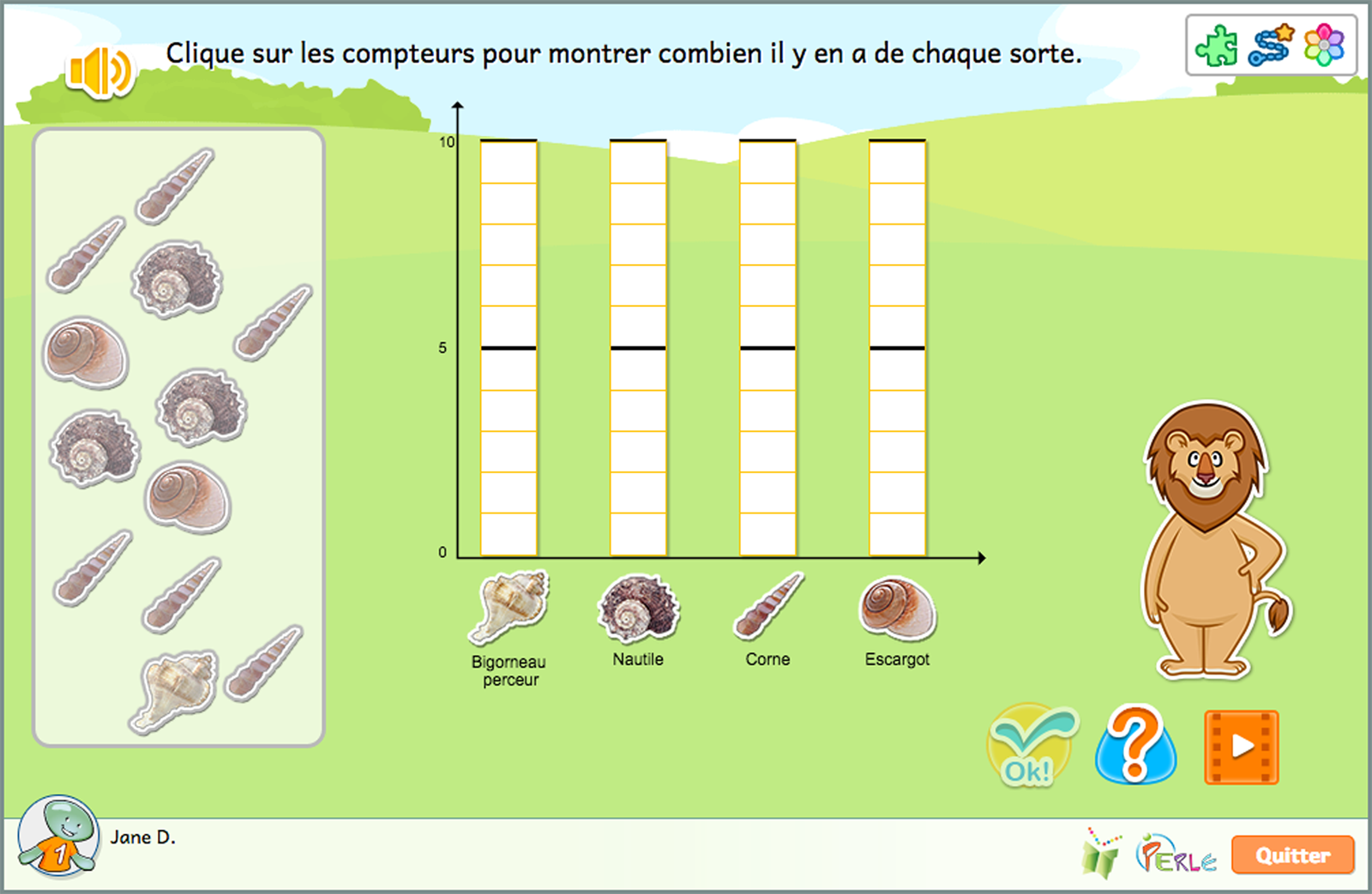
Cette idée a pour objectif de favoriser chez l'élève le développement de ses compétences pour interpréter et illustrer les données au moyen de diagrammes à barres et de tableaux. Le logiciel fournit à l'élève un contexte qui lui demande de compter et d'illustrer les totaux obtenus au moyen d'images, de compteurs et de symboles numériques. L'élève découvre ainsi qu'un diagramme à barre est utile pour organiser des données en catégories afin de connaître d'un coup d'œil les tailles relatives des groupes. Les élèves apprennent également qu'un tableau peut s'avérer utile afin d'obtenir rapidement un total.
L'idée Diagrammes à barre et tableaux comporte deux activités :
- Identifier le nombre de catégories pour un ensemble d'objets donné. Étiqueter un diagramme à barres. Remplir un diagramme à barres de manière à ce qu'il corresponde à l'ensemble d'objets.
- Identifier le nombre de catégories pour une un ensemble d'objets donné. Étiqueter un diagramme à barres. Remplir un diagramme à barres de manière à ce qu'il corresponde à l'ensemble d'objets. Compléter un tableau au moyen des informations d'un diagramme à barres.
Droite numérique
L'idée Droite numérique permet à l'élève d'aborder différemment le concept de nombre exploré précédemment dans le thème du même nom.
En mettant l'accent sur la position à laquelle correspond un nombre sur une droite numérique, le logiciel propose à l'élève une autre méthode concrète pour dénombrer et comparer des nombres et les placer en ordre. La droite numérique aide l'élève à voir que compter vers le haut correspond à une augmentation en quantité et que compter vers le bas correspond à une diminution en quantité.
De plus, l'élève remarque que des déplacements positifs et négatifs correspondent à un mouvement dans des directions opposées le long de la droite numérique, ce qui lui permet de concevoir les concepts d'addition et de soustraction autrement. L'utilisation d'une unité de dimension standard (longueur d'un pas) encourage également l'élève à discuter de l'utilisation de différents systèmes d'unités (p. ex. mm, cm, m, pouce, pied, yard) qui mènent à des réponses correctes et qui sont pourtant différentes sur le plan numérique.
Déplacement numérique

L'idée Déplacement numérique travaille au moyen de trois nombres : le point de départ (a), le déplacement (b) et le point d'arrivée (c), qui sont présentés dans l'équation " a + b = c " ou " a - b = c ". L'élève connaît deux des nombres sur trois. L'élève détermine d'abord l'emplacement auquel chacun des nombres correspond physiquement sur la droite numérique. Puis, l'élève peut utiliser la droite numérique comme support physique afin de déterminer la troisième variable.
L'idée Déplacement numérique comporte une activité :
- Placer un marqueur à la position de départ ou d'arrivée sur la droite numérique. Créer un déplacement en combinant des blocs de 1, 5 ou 10 unités.





