Overview of ELM
ELM helps your child develop a deeper understanding of the basic mathematical concepts for grade 1 as covered in the Quebec Education Program, including number concept, arithmetic, geometry, probability and statistics, data organization, and strategic thinking.
ELM also meets the standards set by the National Council of Teachers of Mathematics (NCTM) in the United States and Canada.
ELM is designed to be engaging and to provide non-threatening, effective feedback on all activities. As your child completed these activities, he or she will earn animal "friends" in the form of online cards.

Themes – Ideas – Steps
ELM is organized into Themes (an overarching branch of mathematics), which are then divided into different Ideas (mathematical concepts). Each Idea has a certain number of Steps that use carefully sequenced activities to build children’s understanding of the concept. Click on any of the icons below to learn more about a Theme and its associated Ideas and Steps.
Number Concept
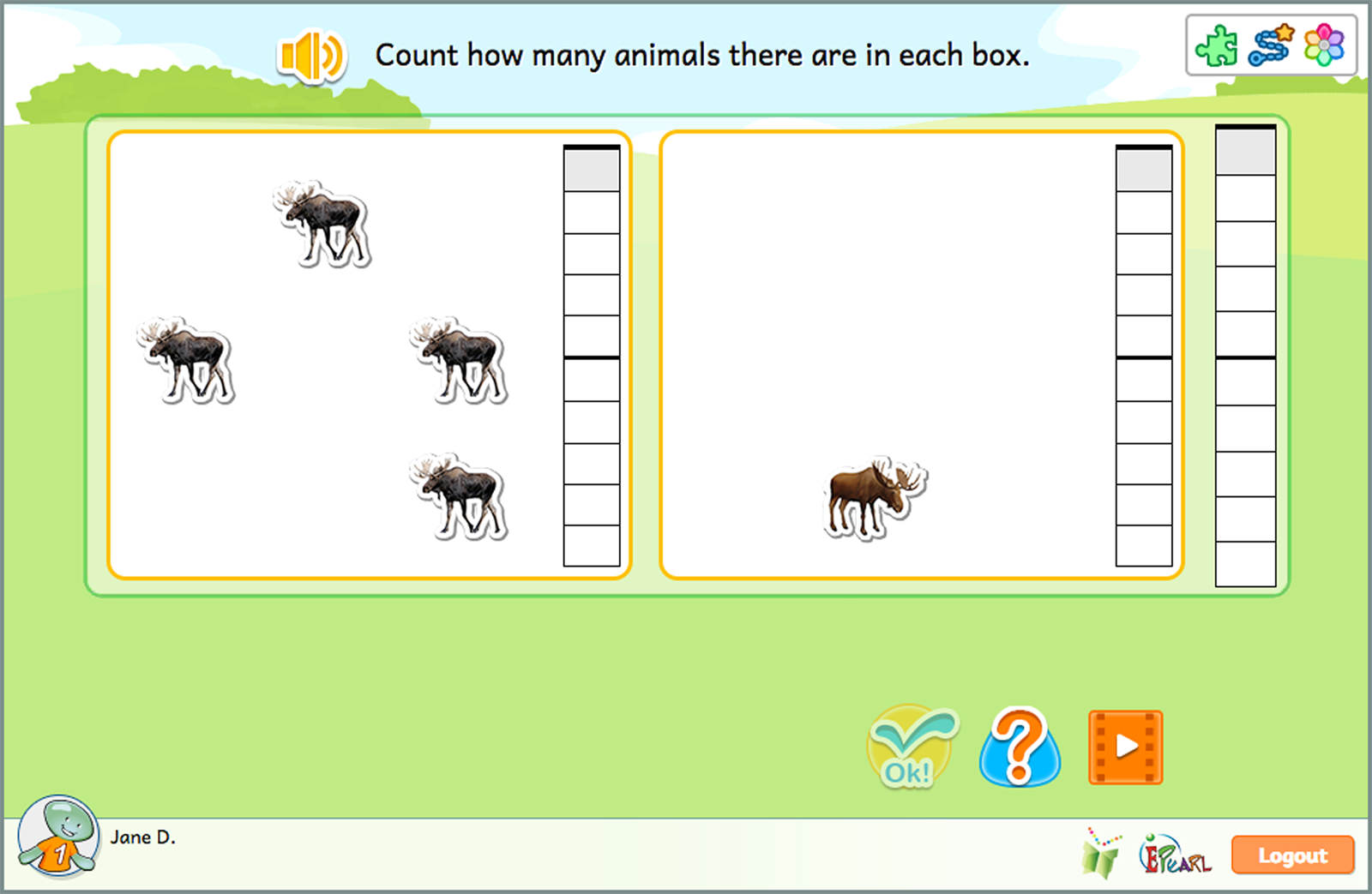
Children are provided with repetitive activities to help them to develop fluency in recognizing, comparing, adding, subtracting, and decomposing numbers. Emphasis is placed on always being able to return to the metaphor of using objects to express an operation with numbers.
Most of the steps in this theme focus on the numbers 1-9. This allows children the opportunity to learn the concept in a way where they can verify the answer for themselves by using their fingers.
Count
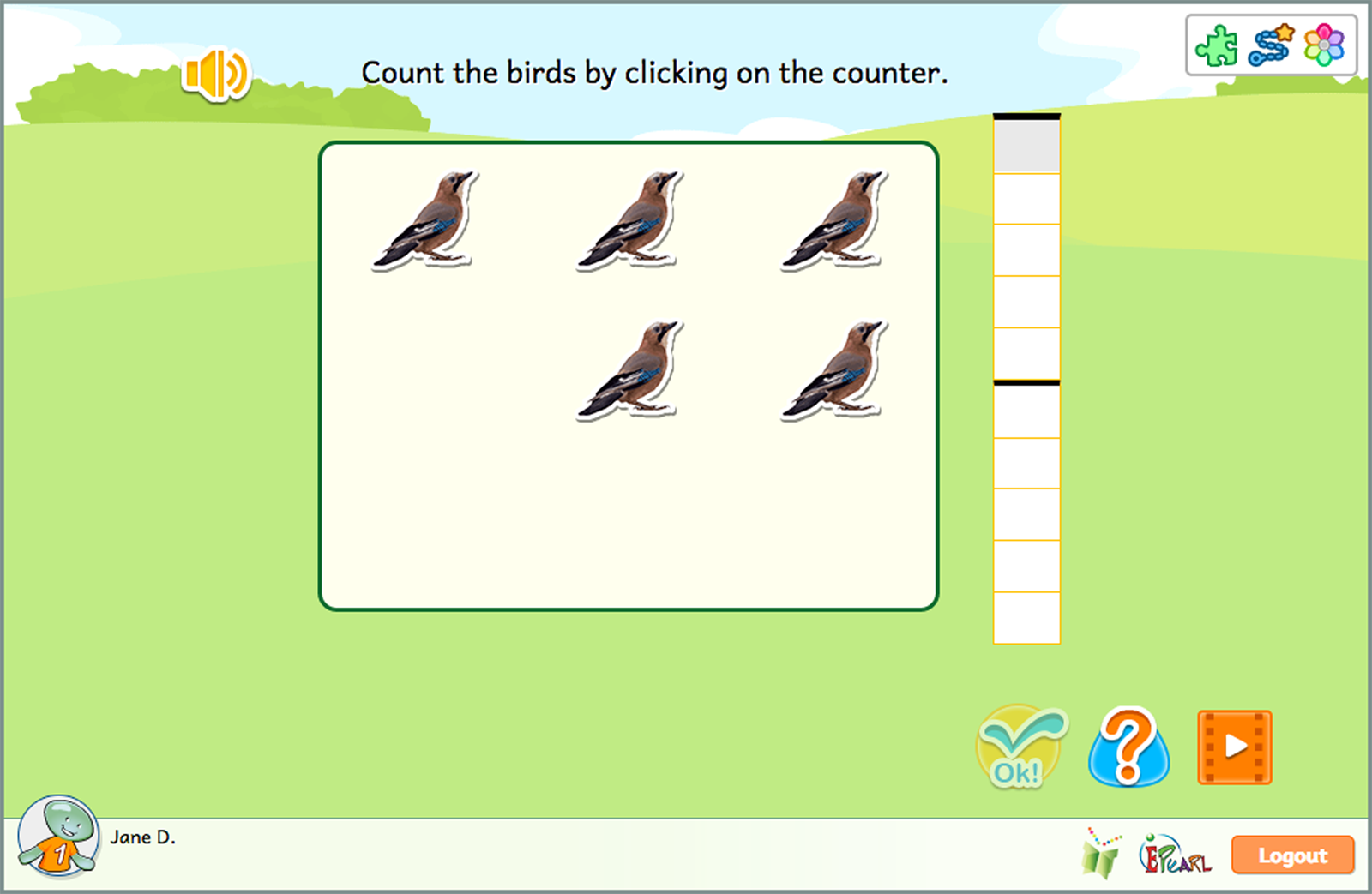
The Count idea has five steps.
These steps help children become familiar with the basic numerals (1 through 9) and the quantity each represents. Steps are structured to move from concrete to abstract means of counting a set of objects.
Count helps children gain fluency at subitizing, an important skill in which they can instantly recognize the number of objects in a set of objects presented without any conscious counting.
Compare
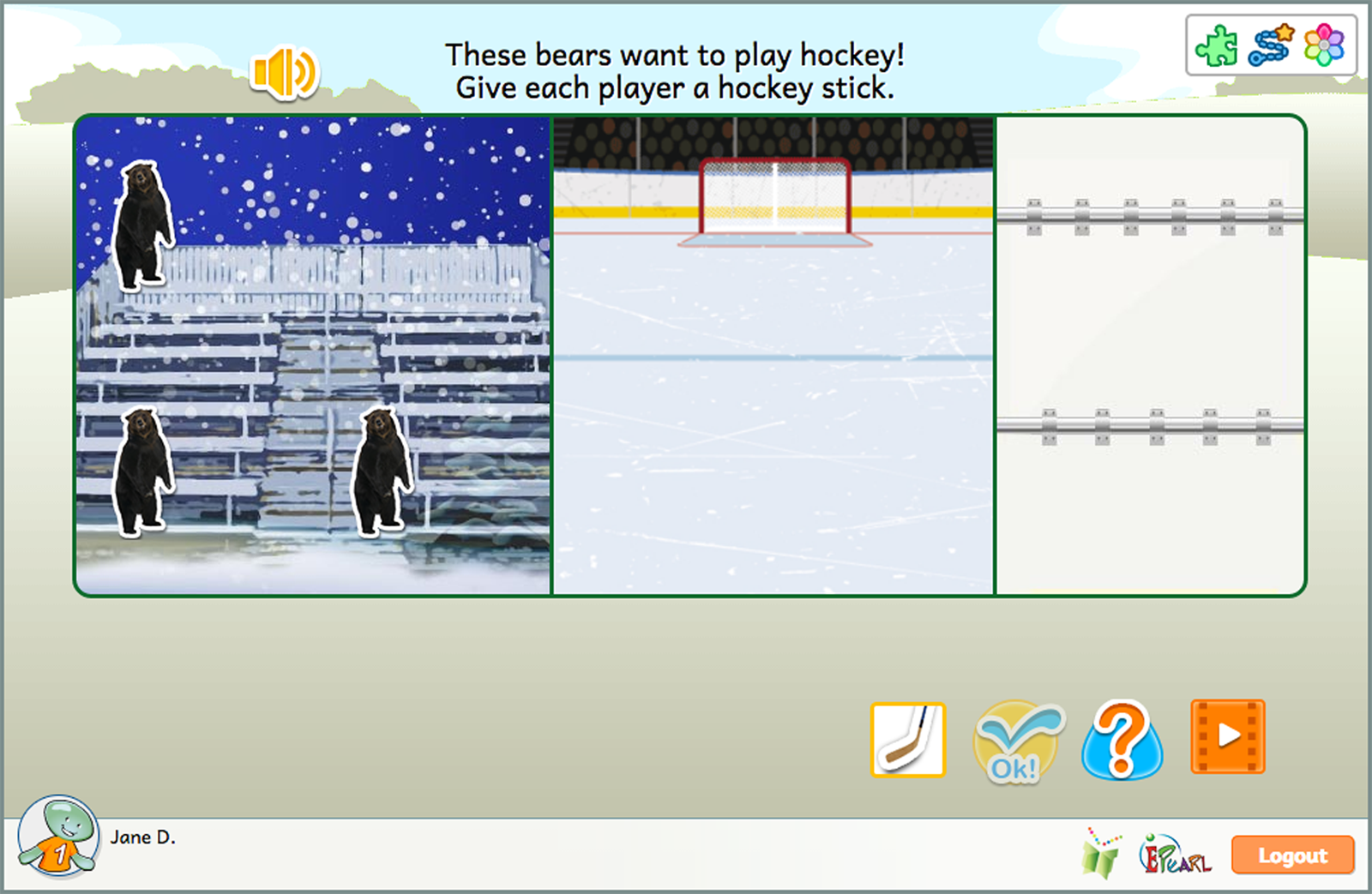
The Compare idea has four steps.
Children are asked to count and then compare two sets of objects: bears and hockey sticks. They then determine if the sets are equal or whether one integer is larger or smaller than the other.
Compare exposes children to both natural language and mathematical symbols that express and compare the cardinality of two sets.
Add
The Add idea has four steps.
Children are asked to add two sets of animals. They eventually learn that the resulting number is the “sum” or “total,” which can be represented by an equation. Children then write these equations by placing the numbers and symbols in the appropriate order.
The steps in Add reuse the counting strategies learned in the Count steps. This includes clicking on objects to count them and the use of counters.
Subtract
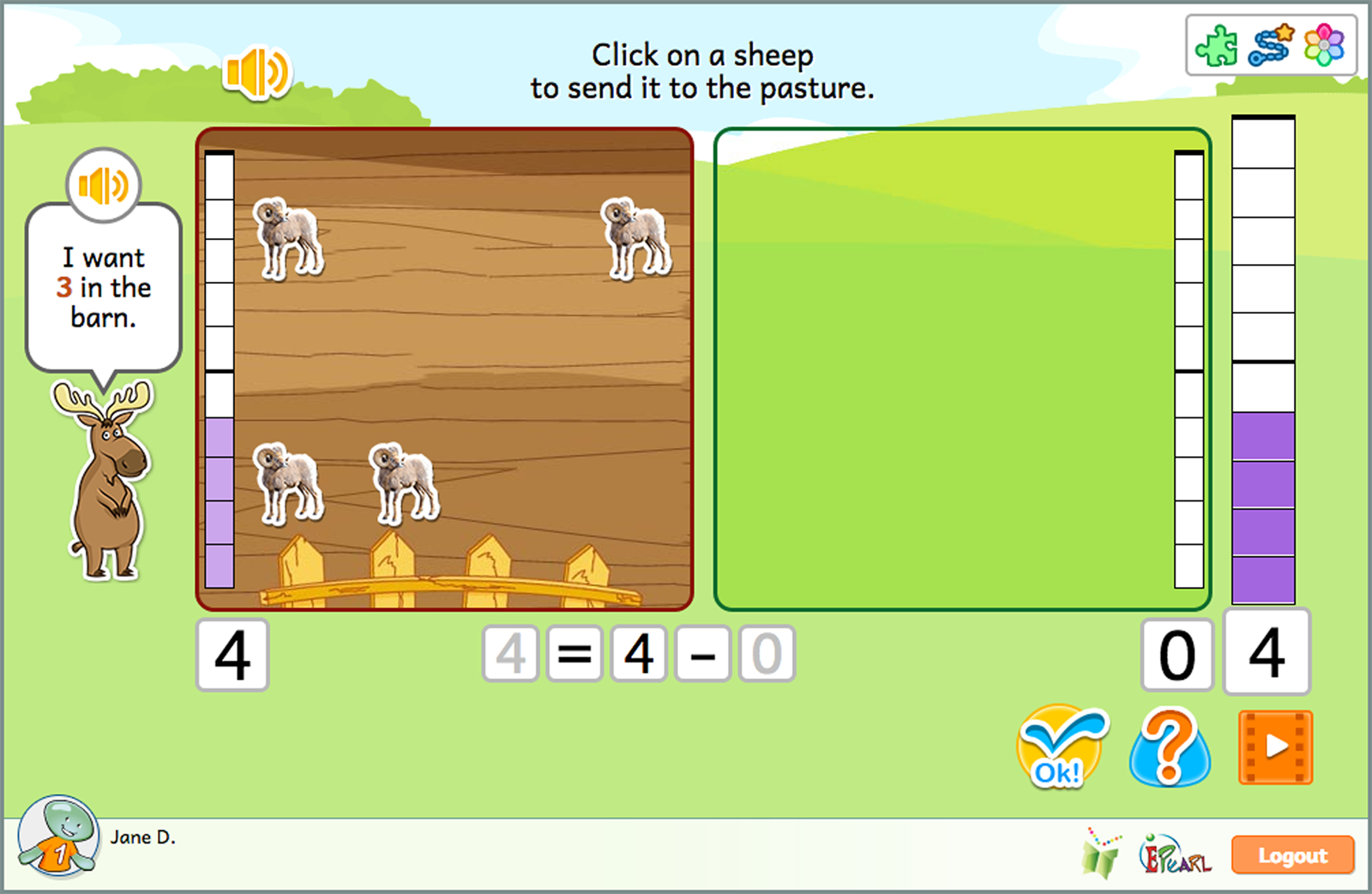
The Subtract idea has five steps.
Subtraction is introduced as the process of taking away. Children first see all animals in one set (the barn). They have to count how many are in the set and note the empty second set (the pasture). Then students subtract by sending animals from the barn to the pasture. Eventually the create equations to show the subtraction.
Decompose

The Decompose idea has four steps.
Children practice decomposing, or partitioning, integers, using a set of beavers. They must separate the beavers into two different sets by deciding which beavers are in the grass or water region. In the final step, children are asked to complete a table to demonstrate their understanding of the different possibilities for decomposing a specific number.
Place Value
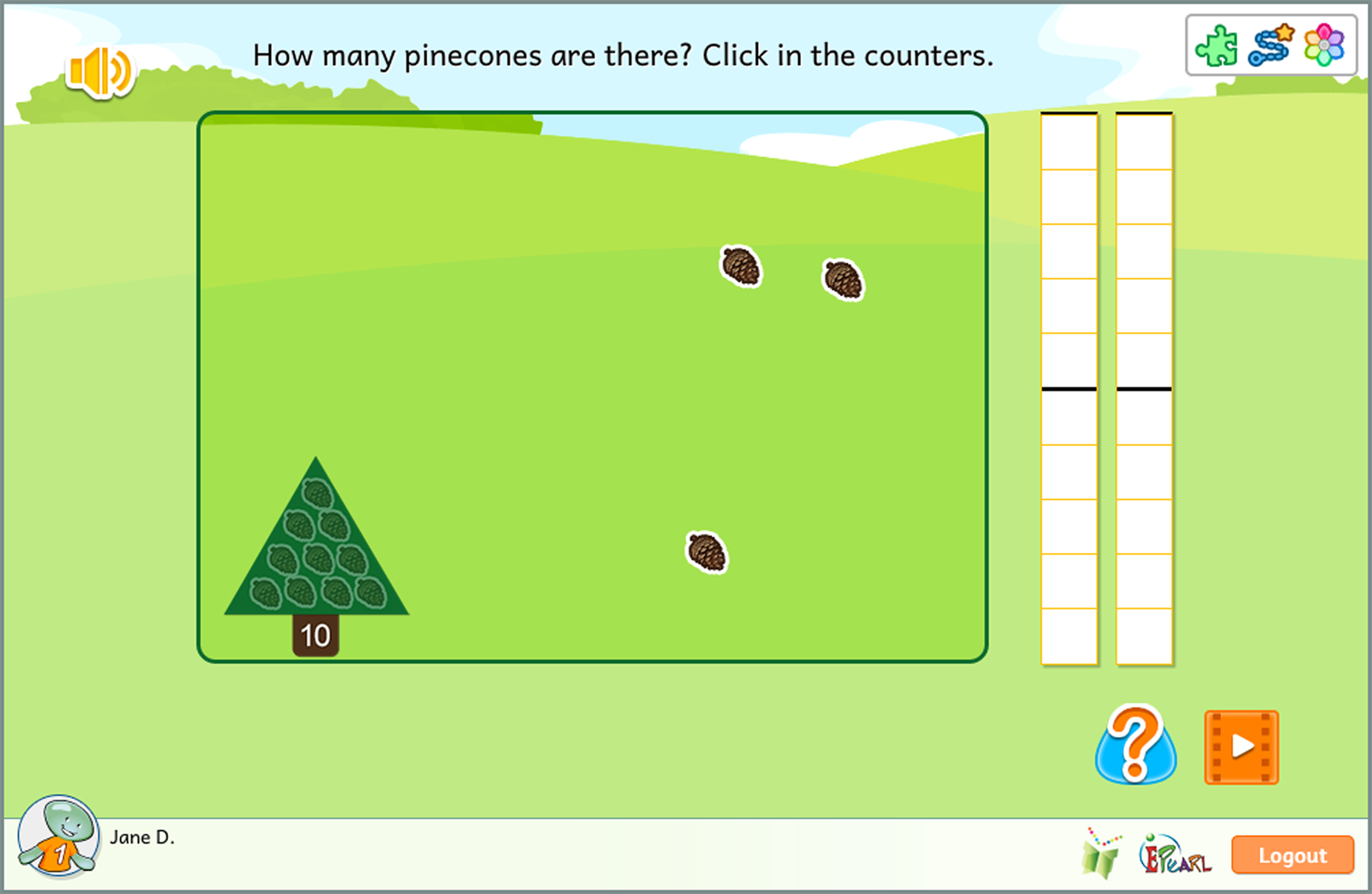
The Place Value idea has nine steps.
This idea helps children realize that numbers beyond 9 but less than 100 have two ‘parts’: there is a number of ‘10s’ combined with a number of ‘1s’. The goal is to have students understand that one ‘ten’ is equal to ten ‘ones’.
In order to facilitate students’ grasping the notion of place value, ELM’s steps associate tens to trees. When ten units - represented as pinecones - are grouped, they become a tree.
Geometry
This theme asks students to categorize and distinguish two-dimensional shapes. ELM’s goal is to develop children’s fluency in recognizing shapes and foster their own criteria for correctly identifying shapes. To this end, ELM does not list a shape’s attributes. Instead, children are provided with varying prototypes and must define their own criteria for what makes a shape a shape. Children also practice identify shapes that have been rotated, which makes them more difficult to recognize.
Identify Shapes
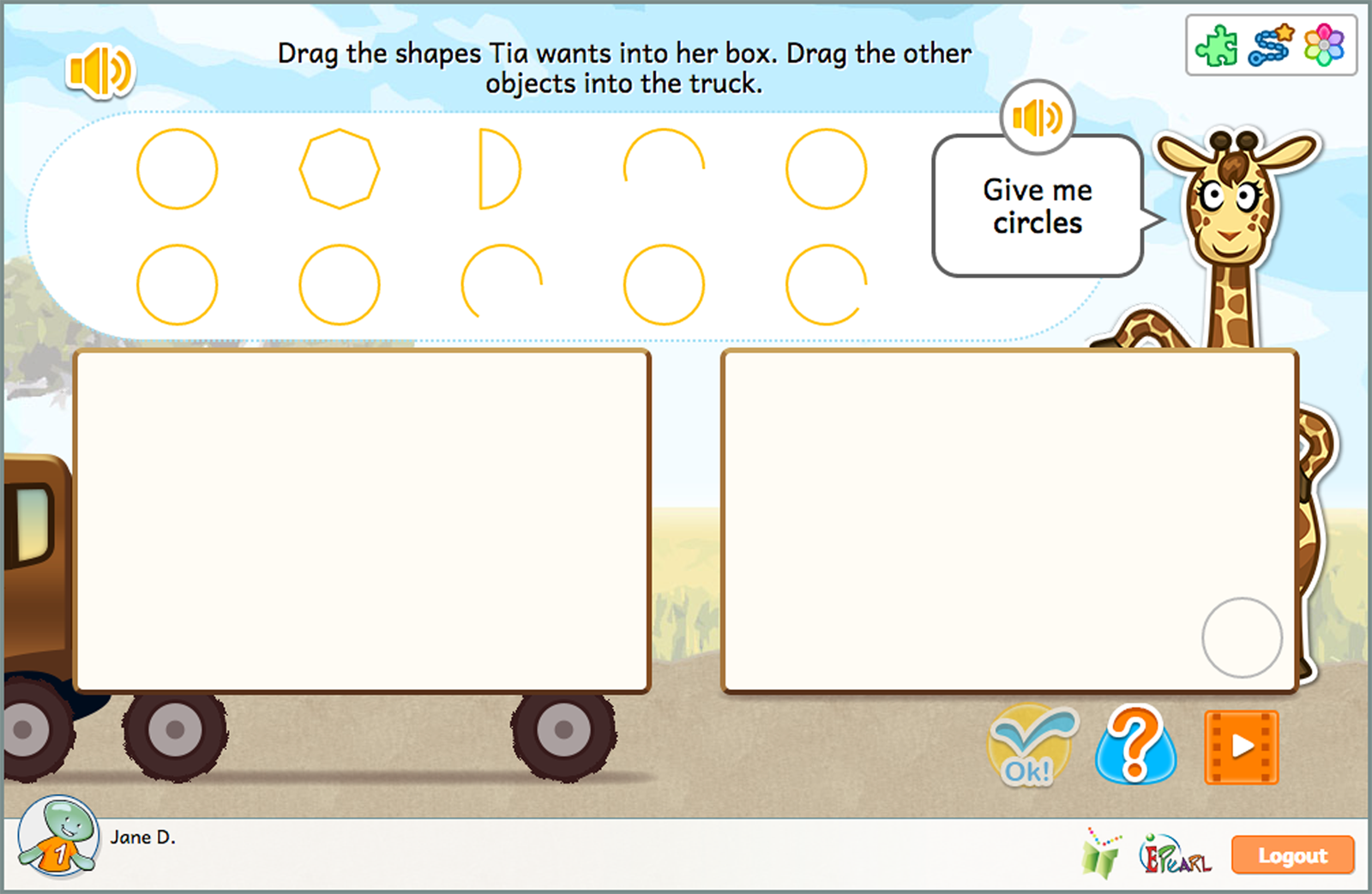
The Identify Shapes idea has three steps.
Children are first asked to sort an array of two-dimensional shapes and open figures. Then, they are asked to identify and sort a specific shape (circle, square, rhombi, rectangle, or triangle). Finally, they are again asked to sort a specific shape, but this time some of the objects will be rotated, thus increasing the activity’s difficulty.
Patterns
This theme helps children develop skills in recognizing the changing attributes in patterns, especially determining the rule for a repeating pattern. Children typically express their understanding by recognizing, continuing, completing and creating patterns. The ELM activities help children identify regularity and building sequences.
Translate Patterns
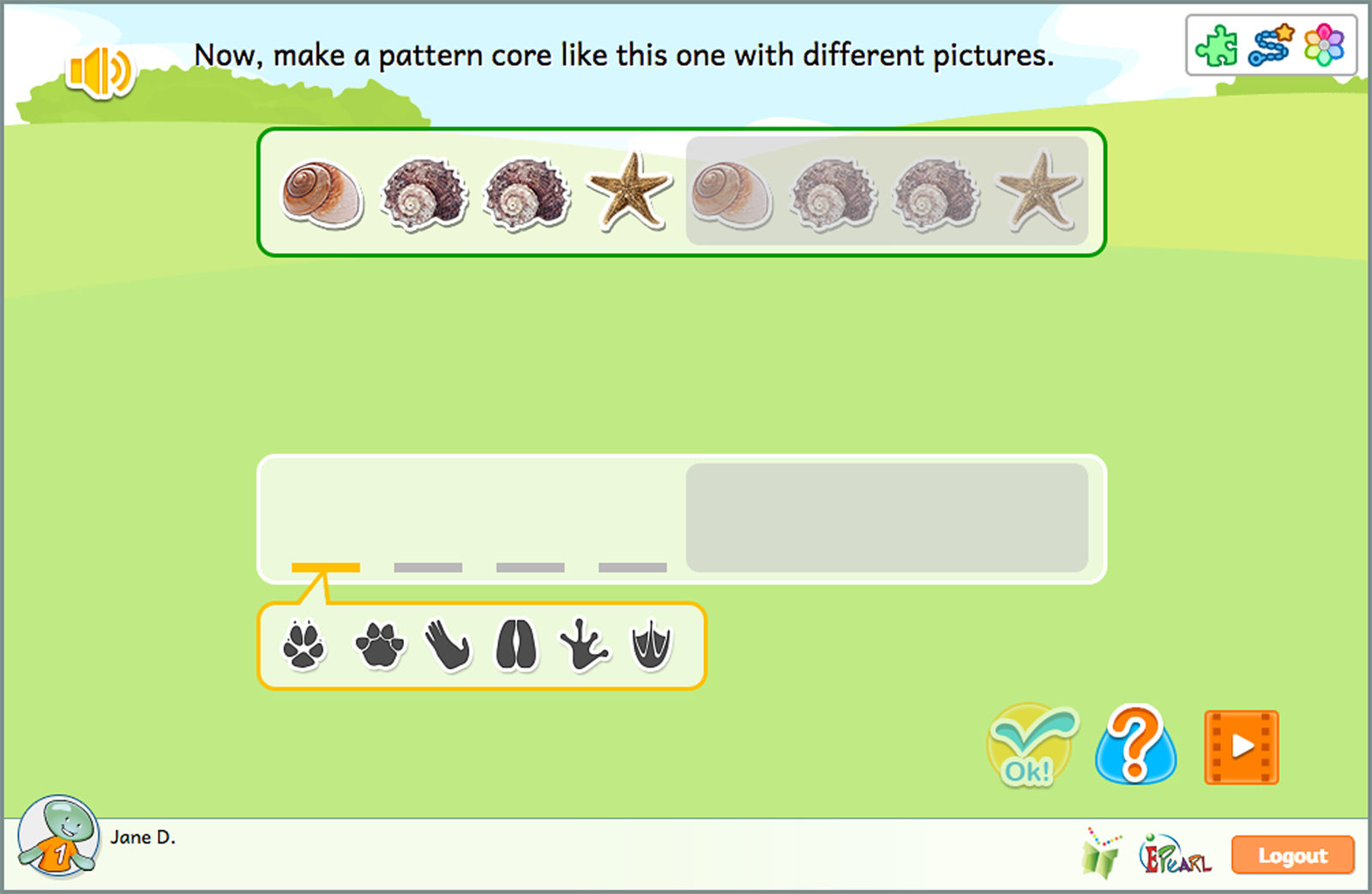
The Translate Patterns has one step.
In the first part, children are asked to is identify the repeating portion – the core, or unit of repeat. Then, children extend this understanding of the core structure by abstracting the pattern, meaning they use a new set of objects to recreate the pattern.
Data
This theme helps children organize and interpret data using graphs and tables. To support children’s development of these skills, the theme presents situations where the answer is not instantly obvious. In order to make sense of the situation, the student is required to organize data according to common attributes and represent a tally using graphs and tables.
Bar Graphs and Tables
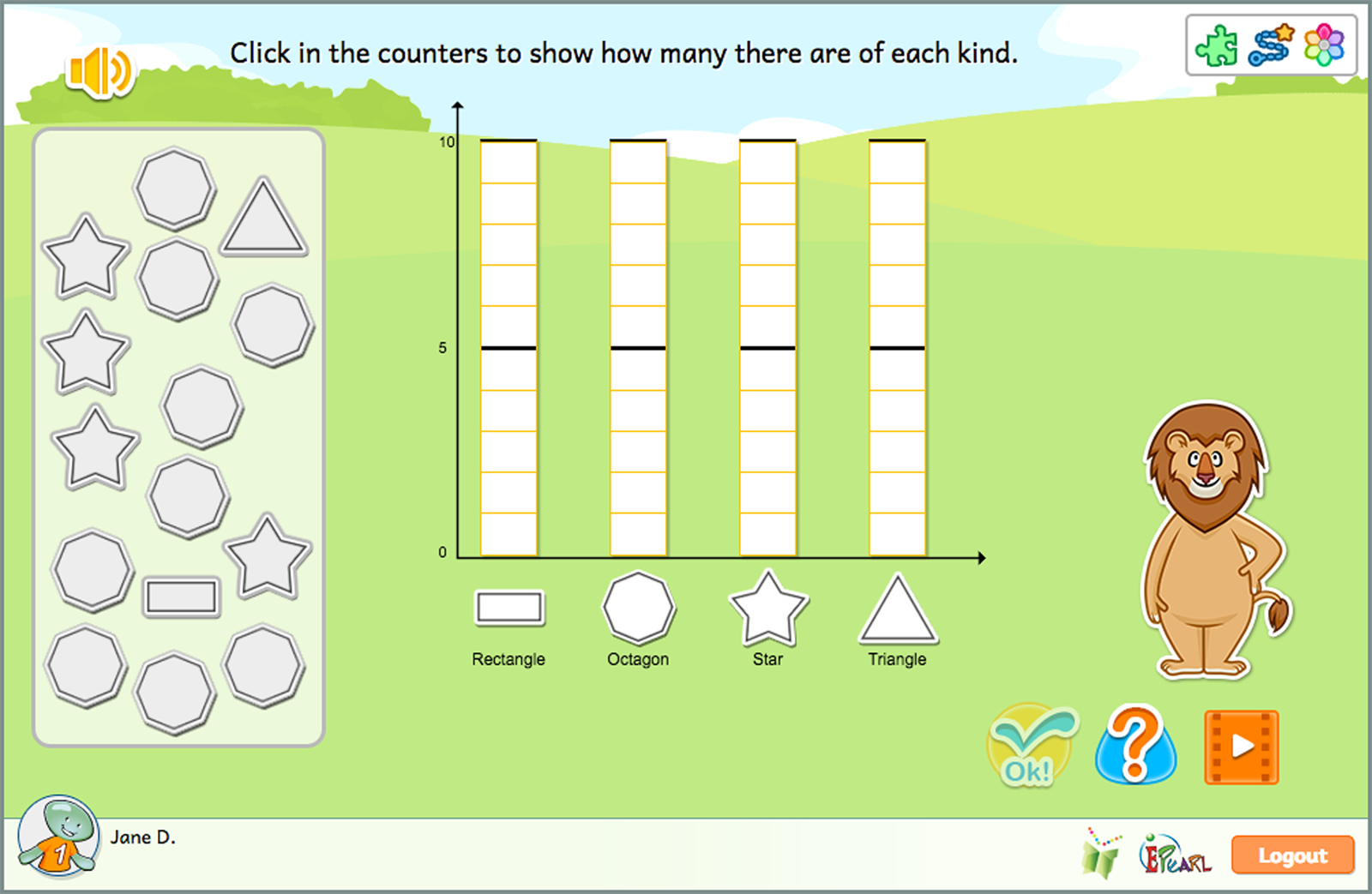
The Bar Graph and Tables idea has two steps.
Children are presented with a pile of objects, consisting of 2-4 categories with a total of 10-15 objects. Children must identify the categories and label a bar graph so each category is represented. The student is then prompted to complete the bar graph in relation to the given pile of objects.
This second step is the same as the first one but also asks children to complete a table at the end, using the information in their bar graph. This demonstrates that both the bar graph and table can be used to represent their data.
Number Line
This theme introduces a number line, which provides children a concrete method for counting, comparing, and ordering numbers. Children see that counting up is related to increases in quantity and counting down is related to decreases in quantity. As well, children gain a new sense of addition and subtraction by visualizing them as displacement along the number line.
Number as Displacement
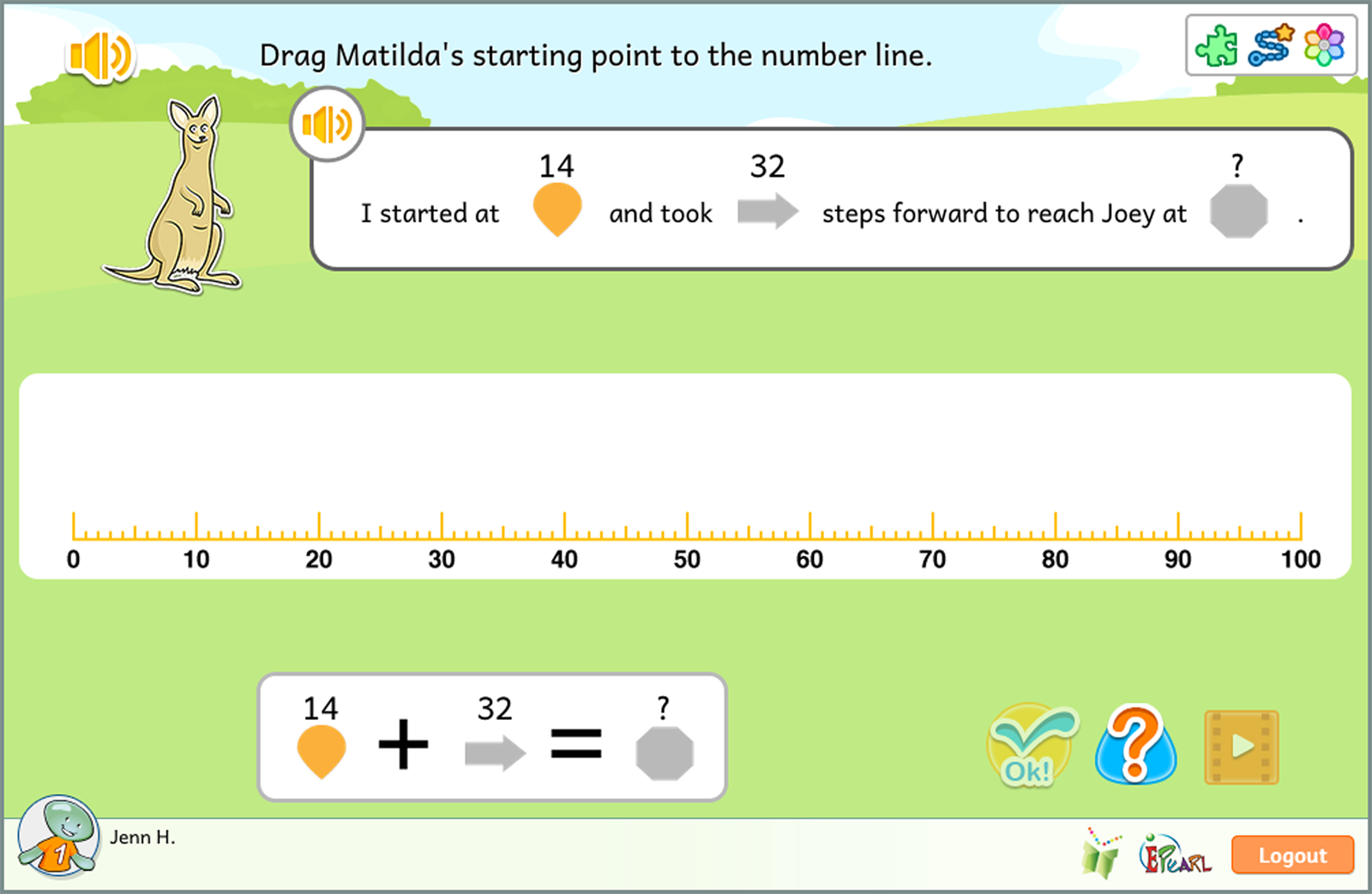
The Number as Displacement idea has one step.
This Idea provides children with a situational problem where three numbers are related. The starting point (a), the displacement (b), and the ending point (c) are presented by the equation “a + b = c” or “a – b = c”. Two out of these three are provided, and the child must find the third.
In the process of using the number line, students may count/add by 1s, 5s, and 10s. They gain proficiency in composing/decomposing numbers while gaining fluency in addition/subtraction with numbers up to 100.





